

| A. | 1 | B. | 2 | C. | 4 | D. | 不能确定 |
分析 过点C作CD⊥AB于D,可得AD=$\frac{1}{2}$AB=1,在Rt△ACD中,利用三角函数的定义算出cosA=$\frac{1}{|AC|}$,再由向量数量积的公式加以计算,可得$\overrightarrow{AB}$•$\overrightarrow{AC}$的值.
解答 解: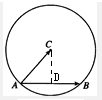 过点C作CD⊥AB于D,则D为AB的中点.
过点C作CD⊥AB于D,则D为AB的中点.
在Rt△ACD中,AD=$\frac{1}{2}$AB=1,
可得cosA=$\frac{AD}{AC}=\frac{1}{|\overrightarrow{AC}|}$,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=$|\overrightarrow{AB}||\overrightarrow{AC}|$cosA=$|\overrightarrow{AB}|•|\overrightarrow{AC}|•\frac{1}{|\overrightarrow{AC}|}$=$|\overrightarrow{AB}|=2$,
故选:B.
点评 本题已知圆的弦长,求向量的数量积.着重考查了圆的性质、直角三角形中三角函数的定义与向量的数量积公式等知识,属于中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | 10,15,25 | B. | 10,16,24 | C. | 11,15,24 | D. | 12,13,25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1+5i}{5}$ | B. | $\frac{-1+7i}{5}$ | C. | 1+i | D. | $\frac{-1+5i}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com