
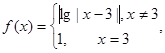 若关于
若关于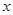 的方程
的方程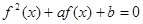 有9个不同实数解,则实数
有9个不同实数解,则实数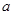 的取值范围是( )
的取值范围是( )| A.(0,1) | B.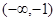 |
C.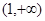 | D. |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
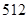 平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?
平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
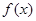 的定义域为
的定义域为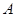 ,若
,若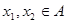 且
且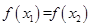 时总有
时总有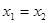 ,则称
,则称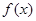 为单函数.下列命题中的真命题是 ( )
为单函数.下列命题中的真命题是 ( )A.函数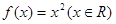 是单函数; 是单函数; |
B.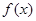 为单函数, 为单函数, 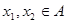 ,若 ,若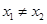 ,则 ,则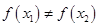 ; ; |
C.若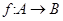 为单函数,则对于任意 为单函数,则对于任意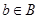 , ,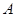 中至少有一个元素与 中至少有一个元素与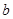 对应; 对应; |
D.函数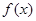 在某区间上具有单调性,则 在某区间上具有单调性,则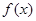 一定是单函数. 一定是单函数. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
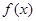 对于任意实数
对于任意实数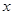 ,存在常数
,存在常数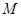 ,使该不等式
,使该不等式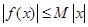 恒成立,就称函数
恒成立,就称函数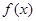 为有界泛涵,下面有4个函数:①
为有界泛涵,下面有4个函数:①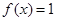 ②
②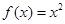
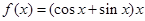 ④
④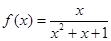 ,其中有两个属于有界泛涵,它们是( )
,其中有两个属于有界泛涵,它们是( )| A.①② | B.②④ | C.①③ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com