
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 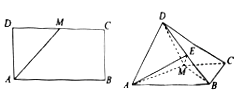
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数 ![]() 的一条对称轴是x=
的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数;
④若 ![]() ,则x1﹣x2=kπ,其中k∈Z;
,则x1﹣x2=kπ,其中k∈Z;
⑤函数f(x)=sinx+2|sinx|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,则k的取值范围为(1,3).
以上五个命题中正确的有(填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如表的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程;(参考公式: ![]() =
= 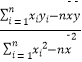 ,
, ![]() =y﹣
=y﹣ ![]() )
)
(2)已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大?(利润=售价﹣收购价)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一元二次不等式f(x)<0的解集为{x|x<﹣1或 ![]() ,则f(ex)>0的解集为( )
,则f(ex)>0的解集为( )
A.{x|x<﹣1或x>﹣ln3}
B.{x|﹣1<x<﹣ln3}
C.{x|x>﹣ln3}
D.{x|x<﹣ln3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为y2=4x,直线L过定点P(﹣2,1),斜率为k.当k为何值时直线与抛物线:
(1)只有一个公共点;
(2)有两个公共点;
(3)没有公共点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com