练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f(x)＝excos x－x.

    (1)求曲线y＝f(x)在点(0，f(0))处的切线方程；

    (2)求函数f(x)在区间上的最大值和最小值．

    【答案】（1）y＝1；（2）最大值为1，最小值为.

    【解析】(1)因为f(x)＝excos x－x，

    所以f′(x)＝ex(cos x－sin x)－1，f′(0)＝0.

    又因为 f(0)＝1，

    所以曲线y＝f(x)在点(0，f(0))处的切线方程为y＝1.

    (2)设h(x)＝ex(cos x－sin x)－1，

    则h′(x)＝ex(cos x－sin x－sin x－cos x)＝－2exsin x.

    当x∈时，h′(x)＜0，

    所以h(x)在区间上单调递减．

    所以对任意x∈有h(x)＜h(0)＝0，

    即f′(x)＜0.

    所以函数f(x)在区间上单调递减．

    因此f(x)在区间上的最大值为f(0)＝1，最小值为f＝－.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数的图象与直线恰有三个不同的交点，则实数的取值范围是_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）当时，求函数的单调区间；

    （2）若对于任意，都有恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若在处取得极值，求的值；

    （2）设，试讨论函数的单调性；

    （3）当时，若存在正实数满足，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，．

    （1）若且，求函数的最小值；

    （2）若对于任意恒成立，求a的取值范围；

    （3）若，求函数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

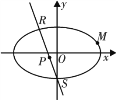
    【题目】如图，椭圆，且点到椭圆C的两焦点的距离之和为.

    (Ⅰ)求椭圆的标准方程；

    (Ⅱ) 若，是椭圆上的两个点，线段的中垂线的斜率为，且直线与交于点，求证：点在直线上.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】手机完全充满电量，在开机不使用的状态下，电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间．

    为了解， 两个不同型号手机的待机时间，现从某卖场库存手机中随机抽取， 两个型号的手机各台，在相同条件下进行测试，统计结果如下，

    手机编号

    型待机时间（）

    型待机时间（）

    其中， ， 是正整数，且．

    （）该卖场有台型手机，试估计其中待机时间不少于小时的台数．

    （）从型号被测试的台手机中随机抽取台，记待机时间大于小时的台数为，求的分布列及其数学期望．

    （）设， 两个型号被测试手机待机时间的平均值相等，当型号被测试手机待机时间的方差最小时，写出， 的值（结论不要求证明）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中a，．

    当时，若在处取得极小值，求a的值；

    当时．

    若函数在区间上单调递增，求b的取值范围；

    若存在实数，使得，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上．

    （）求椭圆的方程．

    （）设动直线与椭圆有且仅有一个公共点，判断是否存在以原点为圆心的圆，满足此圆与相交于两点， （两点均不在坐标轴上），且使得直线、的斜率之积为定值？若存在，求此圆的方程；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案