
【题目】已知函数![]() .
.
(1)判断![]() 的单调性;
的单调性;
(2)已知![]() :不等式
:不等式![]() 对任意
对任意![]() 恒成立;
恒成立;![]() :函数
:函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,如果
内,如果![]() 为真,
为真,![]() 为假,求实数
为假,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() ,且
,且![]() 时,
时,![]() 单调递增;(2)
单调递增;(2)![]() .
.
【解析】
试题分析:(1)由题意可利用分类讨论法进行求解,当![]() 时,有
时,有![]() ,且
,且![]() 为增函数,
为增函数,![]() 为减函数,从而
为减函数,从而![]() 为增函数,所以
为增函数,所以![]() 为增函数,当
为增函数,当![]() 时,
时,![]() ,且
,且![]() 为减函数,
为减函数,![]() 为增函数,从而
为增函数,从而![]() 为减函数,所以
为减函数,所以![]() 为增函数,故当
为增函数,故当![]() ,且
,且![]() 时,
时,![]() 单调递增;(2)由(1)知
单调递增;(2)由(1)知![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 在
在![]() 上的最大值为
上的最大值为![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() ;若函数
;若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,由二分法可得
内,由二分法可得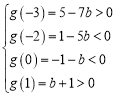 ,得
,得![]() .又因为
.又因为![]() 为真,
为真,![]() 为假,所以
为假,所以![]() 、
、![]() 一真一假,若
一真一假,若![]() 真,
真,![]() 假,则有
假,则有![]() ;若
;若![]() 假,
假,![]() 真,则
真,则![]() .故实数
.故实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)当![]() 时,
时,![]() 为增函数,
为增函数,![]() 为减函数,
为减函数,
从而![]() 为增函数,所以
为增函数,所以![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,
![]() 为减函数,
为减函数,![]() 为增函数,
为增函数,
从而![]() 为减函数,所以
为减函数,所以![]() 为增函数,
为增函数,
故当![]() ,且
,且![]() 时,
时,![]() 单调递增.……………………………………5分
单调递增.……………………………………5分
(2)由(1)知![]() 在
在![]() 上是增函数,则
上是增函数,则
![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
若不等式![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() .……………………7分
.……………………7分
若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,
内,
则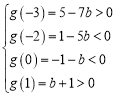 ,得
,得![]() .……………………………………9分
.……………………………………9分
∵![]() 为真,
为真,![]() 为假,∴
为假,∴![]() 、
、![]() 一真一假,
一真一假,
若![]() 真,
真,![]() 假,则有
假,则有![]() ;若
;若![]() 假,
假,![]() 真,则
真,则![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() .…………………………12分
.…………………………12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
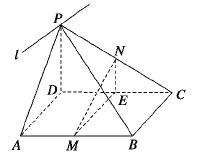
【题目】如图,P为平行四边形ABCD所在平面外一点,MN分别为ABPC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数![]() 万件与每台机器的日产量
万件与每台机器的日产量![]() 万件
万件![]() 之间满足关系:
之间满足关系:![]() .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() .
.
(1)求曲线![]() 的普通方程,并将
的普通方程,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,求
上,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com