
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 时,建造费用最小时
时,建造费用最小时 当
当 时,建造费用最小时
时,建造费用最小时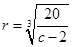 .
.
解析试题分析:(Ⅰ)由圆柱和球的体积的表达式,得到l和r的关系.再由圆柱和球的表面积公式建立关系式,将表达式中的l用r表示.并注意到写定义域时,利用l≥2r,求出自变量r的范围;(Ⅱ)用导数的知识解决,注意到定义域的限制,在区间(0,2]中,极值未必存在,将极值点在区间内和在区间外进行分类讨论.
试题解析:(I)设容器的容积为V,由题意知
故
由于 因此
因此 .3分
.3分
所以建造费用
因此 ..5分
..5分
(II)由(I)得
由于 当
当
令
 ;所以
;所以 .7分
.7分
(1)当 时,
时,
所以 是函数y的极小值点,也是最小值点。 .10分
是函数y的极小值点,也是最小值点。 .10分
(2)当 即
即 时, 当
时, 当 函数单调递减,
函数单调递减,
所以r=2是函数y的最小值点,
综上所述,当 时,建造费用最小时
时,建造费用最小时
当 时,建造费用最小时
时,建造费用最小时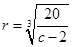 13分
13分
考点:1.函数解析式和定义域;2.函数模型的应用;3.函数最值的求法


科目:高中数学 来源: 题型:解答题
某地开发了一个旅游景点,第1年的游客约为100万人,第2年的游客约为120万人.某数学兴趣小组综合各种因素预测:①该景点每年的游客人数会逐年增加;②该景点每年的游客都达不到130万人.该兴趣小组想找一个函数 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系.
(1)根据上述两点预测,请用数学语言描述函数 所具有的性质;
所具有的性质;
(2)若 =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测;
(3)若 =
= ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, 
 .
.
(1)若 , 函数
, 函数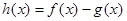 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围;
(2)在(1)的结论下,设函数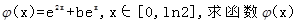 的最小值;
的最小值;
(3)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作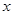 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求出
处的切线平行?若存在,求出 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com