
(2007
湖南,20)已知双曲线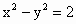 的左、右焦点分别为
的左、右焦点分别为 ,过点
,过点 的动直线与双曲线相交于A、B两点.
的动直线与双曲线相交于A、B两点.
(1)
若动点M满足 (其中O为坐标原点),求点M的轨迹方程;
(其中O为坐标原点),求点M的轨迹方程;
(2)
在x轴上是否存在定点C,使 为常数?若存在,求出点C的坐标;若不存在,请说明理由.
为常数?若存在,求出点C的坐标;若不存在,请说明理由. |
解析:由条件知 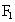 (-2,0), (-2,0),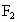 (2,0),设 (2,0),设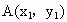 , ,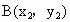 . .
(1) 设M(x,y),则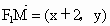 , ,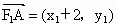 , ,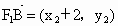 , , .由 .由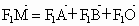 得 得
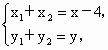
于是 AB的中点坐标为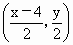 . .
当 AB不与x轴垂直时,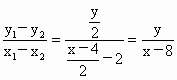 , ,
即 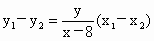 . .
因为 A、B两点在双曲线上,所以 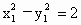 , ,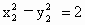 ,两式相减得 ,两式相减得
即 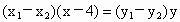 . .
将 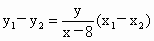 代入上式, 代入上式,
化简得 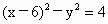 . .
当 AB与x轴垂直时,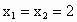 ,求得M(8,0),也满足上述方程. ,求得M(8,0),也满足上述方程.
故点M的轨迹方程是 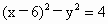 . .
(2) 假设在x轴上存在定点C(m,0),使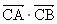 为常数. 为常数.
当 AB不与x轴垂直时,设直线AB的方程是y=k(x-2)(k≠±1).代入 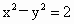 有 有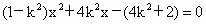 . .
则 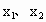 是上述方程的两个实根, 是上述方程的两个实根,
所以 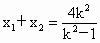 , ,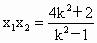 . .
于是 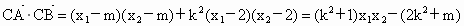
因为 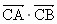 是与k无关的常数,所以4-4m=0,即m=1,此时 是与k无关的常数,所以4-4m=0,即m=1,此时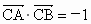 . .
当 AB与x轴垂直时,点A、B的坐标可分别设为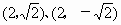 , ,
此时 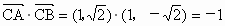 . .
故在 x轴上存在定点C(1,0),使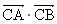 为常数. 为常数. |


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com