
【题目】已知函数![]() .
.
(1)当a=1时,求不等式f(x)>2的解集;
(2)若对任意x∈R,不等式f(x)≥a2-3a-3恒成立,求a的取值范围.
【答案】(1) ![]() .(2) [-1,2+
.(2) [-1,2+![]() ].
].
【解析】
(1)对![]() 分情况讨论,去绝对值处理,从而求解出结果;
分情况讨论,去绝对值处理,从而求解出结果;
(2)对任意x∈R,不等式f(x)≥a2-3a-3恒成立,即求函数![]() ,根据绝对值不等式的性质可得f(x)的最小值为|a|,故原不等式等价于|a|≥a3-3a-3,分情况讨论,进行求解。
,根据绝对值不等式的性质可得f(x)的最小值为|a|,故原不等式等价于|a|≥a3-3a-3,分情况讨论,进行求解。
(1)当a=1时,f(x)=|x-1|+|x-2|.
![]() ,当x≤1时,f(x)=1-x+2-x=3-2x,
,当x≤1时,f(x)=1-x+2-x=3-2x,
由f(x)>2可得,
即![]()
解得x<![]() ;
;
![]() ,当1<x≤2时,f(x)=x-1+2-x=1,
,当1<x≤2时,f(x)=x-1+2-x=1,
此时f(x)>2无解;
![]() ,当x>2时,f(x)=x-1+x-2=2x-3,
,当x>2时,f(x)=x-1+x-2=2x-3,
此时由f(x)>2可得,
即![]() ,
,
解得x>![]() 。
。
综上,可得不等式f(x)>2的解集为![]() 。
。
(2)因为f(x)=|x-a|+|x-2a|≥|(x-a)-(x-2a)|=|a|,
故f(x)取得最小值|a|,
因此原不等式等价于|a|≥a3-3a-3。
![]() ,当a≥0时,有a≥a2-3a-3,
,当a≥0时,有a≥a2-3a-3,
即a2-4a-3≤0,
解得2-![]() ≤a≤2+
≤a≤2+![]() ,
,
此时有0≤a≤2+![]() ;
;
![]() ,当a<0时,有-a≥a2-3a-3,
,当a<0时,有-a≥a2-3a-3,
即a2-2a-3≤0,
解得-1≤a≤3,
此时有-1≤a<0。
综上,可知a的取值范围是[-1,2+![]() ]。
]。


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:
【题目】抚州市某中学利用周末组织教职员工进行了一次秋季登军峰山健身的活动,有![]() 人参加,现将所有参加人员按年龄情况分为
人参加,现将所有参加人员按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如下图所示.已知
等七组,其频率分布直方图如下图所示.已知![]() 之间的参加者有4人.
之间的参加者有4人.
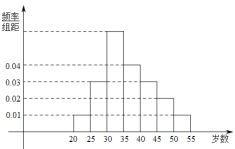
(1)求![]() 和
和![]() 之间的参加者人数
之间的参加者人数![]() ;
;
(2)组织者从![]() 之间的参加者(其中共有
之间的参加者(其中共有![]() 名女教师包括甲女,其余全为男教师)中随机选取
名女教师包括甲女,其余全为男教师)中随机选取![]() 名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
名担任后勤保障工作,求在甲女必须入选的条件下,选出的女教师的人数为2人的概率.
(3)已知![]() 和
和![]() 之间各有
之间各有![]() 名数学教师,现从这两个组中各选取
名数学教师,现从这两个组中各选取![]() 人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有
人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有![]() 名数学教师的概率?
名数学教师的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】珠海市某学校的研究性学习小组,对昼夜温差(最高温度与最低温度的差)大小与绿豆种子一天内出芽数之间的关系进行了研究,该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的![]() 颗绿豆种子当天内的出芽数(如图2)
颗绿豆种子当天内的出芽数(如图2)
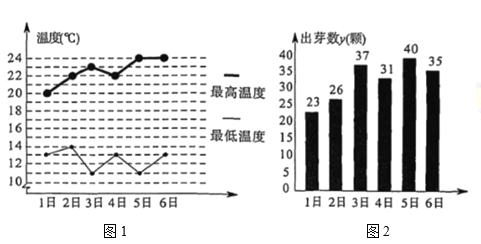
已知绿豆种子出芽数![]() (颗) 和温差
(颗) 和温差![]() 具有线性相关关系.
具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() 的回归方程
的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为![]() ,估计4月7日浸泡的
,估计4月7日浸泡的![]() 颗绿豆种子一天内的出芽数.
颗绿豆种子一天内的出芽数.
附: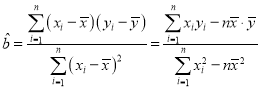 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对相关系数r来说,下列说法正确的是( ).
A.![]() ,
,![]() 越接近0,相关程度越大;
越接近0,相关程度越大;![]() 越接近1,相关程度越小
越接近1,相关程度越小
B.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越大,相关程度越小
越大,相关程度越小
C.![]() ,
,![]() 越接近1,相关程度越大;
越接近1,相关程度越大;![]() 越接近0,相关程度越小
越接近0,相关程度越小
D.![]() ,
,![]() 越接近1,相关程度越小;
越接近1,相关程度越小;![]() 越大,相关程度越大
越大,相关程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() 是棱
是棱![]() 上动点,下列说法正确的是( )
上动点,下列说法正确的是( )
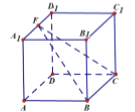
A. 对任意动点![]() ,在平面
,在平面![]() 内不存在与平面
内不存在与平面![]() 平行的直线
平行的直线
B. 对任意动点![]() ,在平面
,在平面![]() 内存在与平面
内存在与平面![]() 垂直的直线
垂直的直线
C. 当点![]() 从
从![]() 运动到
运动到![]() 的过程中,
的过程中,![]() 与平面
与平面![]() 所成的角变大
所成的角变大
D. 当点![]() 从
从![]() 运动到
运动到![]() 的过程中,点
的过程中,点![]() 到平面
到平面![]() 的距离逐渐变小
的距离逐渐变小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() ,
,![]() 、
、![]() 分别为
分别为![]() 的外心,重心,
的外心,重心,![]() .
.
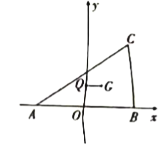
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点且满足
两点且满足![]() ,若存在求出
,若存在求出![]() 的方程,若不存在请说明理由.
的方程,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顾客请一位工艺师把![]() 、
、![]() 两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
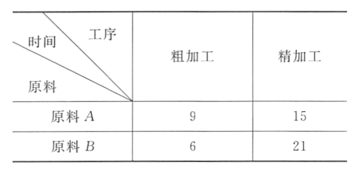
则最短交货期为_______个工作日.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是

A. 2018年3月至2019年3月全国居民消费价格同比均上涨
B. 2018年3月至2019年3月全国居民消费价格环比有涨有跌
C. 2019年3月全国居民消费价格同比涨幅最大
D. 2019年3月全国居民消费价格环比变化最快
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com