
【题目】设函数![]() .
.
(1)求函数的零点;
(2)当![]() 时,求证:
时,求证:![]() 在区间
在区间![]() 上单调递减;
上单调递减;
(3)若对任意的正实数![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)证明见解析;(3)![]()
【解析】
(1)讨论![]() ,
,![]() 且
且![]() ,
,![]() ,解方程可得零点;
,解方程可得零点;
(2)可令![]() ,运用单调性的定义,证得
,运用单调性的定义,证得![]() 在
在![]() 递减,可得
递减,可得![]() ,即可得到证明;
,即可得到证明;
(3)由题意可得![]() ,由绝对值的含义,化简
,由绝对值的含义,化简![]() ,得到在
,得到在![]() 的单调性,即有
的单调性,即有![]() ,运用绝对值不等式的性质,可得
,运用绝对值不等式的性质,可得![]() 的最大值,即可得到
的最大值,即可得到![]() 的范围.
的范围.
解:(1)当![]() 时,
时,![]() 的零点为
的零点为![]() ;
;
当![]() 且
且![]() 时,由
时,由![]() 得
得![]() ,
,
由一元二次方程求根公式得,![]() 的零点为
的零点为![]() ;
;
当![]() 时,方程
时,方程![]() 中的判别式
中的判别式![]() ,故
,故![]() 无零点;
无零点;
(2)证明:当![]() 时,
时,![]() ,可令
,可令![]() ,
,
任取![]() ,
,![]()
![]() ,
,
由![]() ,可得
,可得![]() ,
,![]() ,进而
,进而![]() ,
,
即![]() ,可得
,可得![]() 在
在![]() 上递减,
上递减,
可得![]() 时,
时,![]() ,
,
则![]() ,
,
即![]() 在区间
在区间![]() 上单调递减;
上单调递减;
(3)对任意的正实数![]() ,总存在
,总存在![]() ,
,![]() ,使得
,使得![]() ,则
,则![]() ,
,
当![]() 时,
时,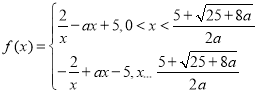 ,
,
则![]() 在
在![]() 递减,在
递减,在![]() ,
,![]() 递增,
递增,
可得![]() ,
,
由于![]() ,设
,设![]() ,可得
,可得![]() ,
,![]() ,
,
可得![]() ,即有
,即有![]() ,可得
,可得![]() ,
,
则![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
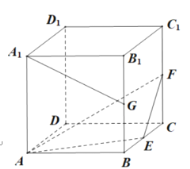
【题目】如图正方体![]() 的棱长为
的棱长为![]() ,
,![]() 、
、![]() 、
、![]() ,分别为
,分别为![]() 、
、![]() 、
、![]() 的中点.则下列命题:①直线
的中点.则下列命题:①直线![]() 与平面
与平面![]() 平行;②直线
平行;②直线![]() 与直线
与直线![]() 垂直;③平面
垂直;③平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]() ;④点
;④点![]() 与点
与点![]() 到平面
到平面![]() 的距离相等;⑤平面
的距离相等;⑤平面![]() 截正方体所得两个几何体的体积比为
截正方体所得两个几何体的体积比为![]() .其中正确命题的序号为_______.
.其中正确命题的序号为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国已进入新时代中国特色社会主义时期,人民生活水平不断提高,某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为![]() 元)的情况,并根据统计数据制成如下频率分布直方图.
元)的情况,并根据统计数据制成如下频率分布直方图.

(1)根据频率分布直方图估算![]() 的平均值
的平均值![]() ;
;
(2)视样本中的频率为概率,现从该市所有住户中随机抽取![]() 次,每次抽取
次,每次抽取![]() 户,每次抽取相互独立,设
户,每次抽取相互独立,设![]() 为抽出
为抽出![]() 户中
户中![]() 值不低于
值不低于![]() 元的户数,求
元的户数,求![]() 的分布列和期望
的分布列和期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com