
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用已知条件求出双曲线方程,然后通过其它体积求出双曲线的标准方程,即可判断选项.
解答 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1满足彖件:(1)焦点为F1(-5,0),F2(5,0);(2)离心率为$\frac{5}{3}$,
可得c=5,a=3,可得b=4,
可得双曲线方程为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1满足彖件:(1)焦点为F1(-5,0),F2(5,0);①双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意点P都满足||PF1|-|PF2||=6,可得c=5,a=3,可得b=4,
可得双曲线方程为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$.①满足题意.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1满足彖件:(1)焦点为F1(-5,0),F2(5,0);②双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的虚轴长为4,可得b=2,显然不满足题意.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1满足彖件:(1)焦点为F1(-5,0),F2(5,0);③双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个顶点与抛物线y2=6x的焦点重合,抛物线的焦点坐标($\frac{3}{2}$,0),a=$\frac{3}{2}$≠3,显然不满足题意.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1满足彖件:(1)焦点为F1(-5,0),F2(5,0);④双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为4x±3y=0.可得$\frac{b}{a}=\frac{4}{3}$,c=5,解得a=3可得b=4,
可得双曲线方程为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$.
故选:B.
点评 本题考查双曲线的简单性质,标准方程的求法,命题的真假的判断,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
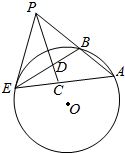 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 0 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0)∪(3,+∞) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(0,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com