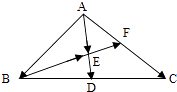
【题目】如图所示，在△ABC中，D、F分别是BC、AC的中点， 
= 
， 
= 
， 
= 
． 
（1）用 、 表示向量 
、 、 
、 
、 
；
（2）求证：B、E、F三点共线．
【答案】
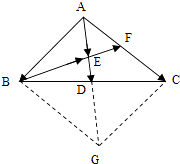
（1）解：如图所示：解延长AD到G，使 
= 
，
连接BG、CG，得到四边形ABGC，
∵D是BC和AG的中点，
∴四边形ABGC是平行四边形，则 
= 
+ 
= 
，
∴ = = 
（ ）， 
= 
= 
（ ）．
∵F是AC的中点，∴ 
= 
= 
，
∴ 
= ﹣ = （ ）﹣ 
= （ 
）．
= ﹣ = ﹣ = （ ）
（2）证明：由（1）可知， = （ ）， = （ ）．
∴ = 
，即 、 是共线向量，所以B、E、F三点共线
【解析】（1）由题意作出辅助线构成平行四边形ABGC，由四边形法则和D是AG的中点求出 ，由题意求出 ，由F是AC的中点求出 ，再由向量减法的三角形法则求出 和 ；（2）由（1）求出 = ，故两个向量共线，即B、E、F三点共线．
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，其离心率为
.
（1）求椭圆
的方程；
（2）直线
与
相交于
两点，在
轴上是否存在点
，使
为正三角形，若存在，求直线
的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若f（x）=x3+ax2+bx+c有两个极值点x1 ， x2且f（x1）=x1 ， 则关于x的方程3[（f（x）]2+2af（x）+b=0的不同实根个数为（ ）
A.2
B.3
C.4
D.不确定
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的奇函数，f（x+2）=f（x），当x∈（0，1]时，f（x）=1﹣2|x﹣ 
|，则函数g（x）=f[f（x）]﹣ 
x在区间[﹣2，2]内不同的零点个数是（ ）
A.5
B.6
C.7
D.9
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）对任意的a，b∈R，都有f（a+b）=f（a）+f（b）﹣1，且当x＞0时，f（x）＞1
（1）判断并证明f（x）的单调性；
（2）若f（4）=3，解不等式f（3m2﹣m﹣2）＜2．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下表是某厂的产量x与成本y的一组数据：
产量x（千件） | 2 | 3 | 5 | 6 |
成本y（万元） | 7 | 8 | 9 | 12 |
（Ⅰ）根据表中数据，求出回归直线的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
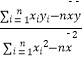（Ⅱ）预计产量为8千件时的成本．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ex ， g（x）=ln 
的图象分别与直线y=m交于A，B两点，则|AB|的最小值为（ ）
A.2
B.2+ln2
C.e2 
D.2e﹣ln 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
