
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,其右焦点F到其右准线的距离为1,离心率为
,其右焦点F到其右准线的距离为1,离心率为![]() ,A,B分别为椭圆
,A,B分别为椭圆![]() 的上、下顶点,过点F且不与x轴重合的直线l与椭圆
的上、下顶点,过点F且不与x轴重合的直线l与椭圆![]() 交于C,D两点,与y轴交于点P,直线
交于C,D两点,与y轴交于点P,直线![]() 与
与![]() 交于点Q.
交于点Q.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
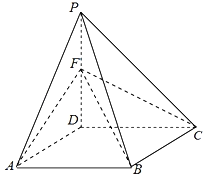
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点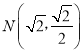 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合S,T,S![]() N*,T
N*,T![]() N*,S,T中至少有两个元素,且S,T满足:
N*,S,T中至少有两个元素,且S,T满足:
①对于任意x,y![]() S,若x≠y,都有xy
S,若x≠y,都有xy![]() T
T
②对于任意x,y![]() T,若x<y,则
T,若x<y,则![]()
![]() S;
S;
下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中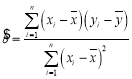 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com