
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②比较![]() 与
与![]() 的大小;
的大小;
(2)当![]() 时,若对
时,若对![]() 时,
时,![]() ,且
,且![]() 有唯一零点,证明:
有唯一零点,证明:![]() .
.
【答案】(1)①见解析,②见解析;(2)见解析
【解析】
(1)①把![]() 代入函数解析式,求出函数的导函数得到
代入函数解析式,求出函数的导函数得到![]() ,再求出
,再求出![]() ,利用直线方程的点斜式求函数
,利用直线方程的点斜式求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
②令![]() ,利用导数研究函数的单调性,可得当
,利用导数研究函数的单调性,可得当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)由题意,![]() ,
,![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .利用导数可得当
.利用导数可得当![]() 时,
时,![]() 在
在![]() 上单调递减,当
上单调递减,当![]() ,
,![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,得到
上单调递增,得到![]() .由
.由![]() 在
在![]() 恒成立,且
恒成立,且![]() 有唯一解,可得
有唯一解,可得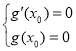 ,得
,得![]() ,即
,即![]() .令
.令![]() ,则
,则![]() ,再由
,再由![]() 在
在![]() 上恒成立,得
上恒成立,得![]() 在
在![]() 上单调递减,进一步得到
上单调递减,进一步得到![]() 在
在![]() 上单调递增,由此可得
上单调递增,由此可得![]() .
.
解:(1)①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 切线方程为
切线方程为![]() ,即
,即![]() ;
;
②令![]() ,
,
则![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
证明:(2)由题意,![]() ,
,
而![]() ,
,
令![]() ,解得
,解得![]() .
.
![]() ,
,![]()
![]() ,
,
![]() 在
在![]() 上有唯一零点
上有唯一零点![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() ,
,![]() 时,
时,![]() ,
,![]() 在
在![]() ,
,![]() 上单调递增.
上单调递增.
![]() .
.
![]() 在
在![]() 恒成立,且
恒成立,且![]() 有唯一解,
有唯一解,
![]()
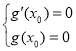 ,即
,即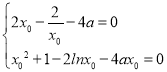 ,
,
消去![]() ,得
,得![]() ,
,
即![]() .
.
令![]() ,则
,则![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
, ![]() ,
,
![]() .
.
![]() 在
在![]() 上单调递增,
上单调递增,
![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为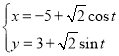 (
(![]() 是参数)以原点
是参数)以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和的直线
的普通方程和的直线![]() 直角坐标方程;
直角坐标方程;
(2)设直线![]() 与
与![]() 轴交点分别是
轴交点分别是![]() ,点
,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会(以下简称武汉军运会)专题新闻发布会在武汉举行,武汉军运会会徽、吉祥物正式公布.武汉军运会将于![]() 年
年![]() 月
月![]() 日举行,赛期
日举行,赛期![]() 天.若将
天.若将![]() 名志愿者分配到两个运动场馆进行服务,每个运动场馆至少
名志愿者分配到两个运动场馆进行服务,每个运动场馆至少![]() 名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
名志愿者,则其中志愿者甲、乙或甲、丙被分到同一场馆的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机软件研发公司为改进产品,对软件用户每天在线的时间进行调查,随机抽取40名男性与20名女性对其每天在线的时间进行了调查统计,并绘制了如图所示的条形图,其中每天的在线时间4h以上(包括4h)的用户被称为“资深用户”.
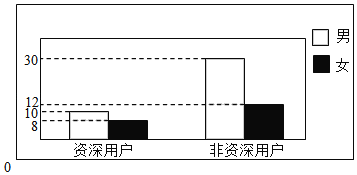
(1)根据上述样本数据,完成下面的2×2列联表,并判定是否有95%的把握认为是否为“资深用户”与性别有关;
“资深用户” | 非“资深用户” | 总计 | |
男性 | |||
女性 | |||
总计 |
(2)用样本估计总体,若从全体用户中随机抽取3人,设这3人中“资深用户”的人数为X,求随机变量X的分布列与数学期望.
附: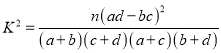 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若满足
,若满足![]() ,则称函数
,则称函数![]() 为“
为“![]() 型函数”.
型函数”.
(1)判断函数![]() 和
和![]() 是否为“
是否为“![]() 型函数”,并说明理由;
型函数”,并说明理由;
(2)设函数![]() ,记
,记![]() 为函数
为函数![]() 的导函数.
的导函数.
①若函数![]() 的最小值为1,求
的最小值为1,求![]() 的值;
的值;
②若函数![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com