
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点. 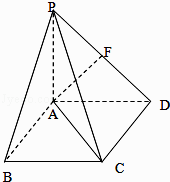
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.
【答案】
(1)解:∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD,
∵正方形ABCD中,CD⊥AD,PA∩AD=A,
∴CD⊥平面PAD,
∴CD⊥AF,
∵PA=AD,FP=FD
∴AF⊥PD
又∵CD∩PD=D
∴AF⊥平面PDC
(2)解:连接CF
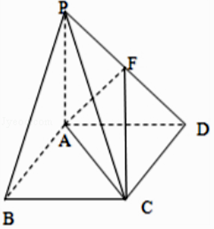
由(1)可知CF是AF在平面PCD内的射影
∴∠ACF是AF与平面PCD所成的角
∵AF⊥平面PDC∴AF⊥FC
在△ACF中, ![]()
∴ ![]()
AF与平面PCD所成的角为30°
【解析】(1)由已知先证明CD⊥平面PAD,可得:CD⊥AF,结合AF⊥PD,可得AF⊥平面PDC;(2)连接CF,由(1)可知CF是AF在平面PCD内的射影,故∠ACF是AF与平面PCD所成的角,解得答案.
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则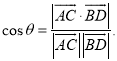 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上. (Ⅰ)求异面直线D1E与A1D所成的角;
(Ⅱ)若二面角D1﹣EC﹣D的大小为45°,求点B到平面D1EC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N. 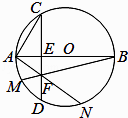
(1)求证:B、E、F、N四点共圆;
(2)求证:AC2+BFBM=AB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为: 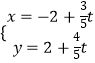 (t为参数),它与曲线C:(y﹣2)2﹣x2=1交于A,B两点.
(t为参数),它与曲线C:(y﹣2)2﹣x2=1交于A,B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1小时、2小时,加工一件乙产品所需工时分别为2小时、1小时,A、B两种设备每月有效使用台时数分别为400小时和500小时.如何安排生产可使月收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | a | 0.9 |
第3组 | [35,45) | 27 | x |
第4组 | [45,55) | b | 0.36 |
第5组 | [55,65) | 3 | y |
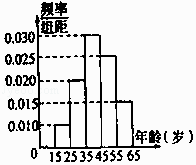
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}的前n项和为Sn , 且a2a3=a5 , S4=10S2 .
(1)求数列{an}的通项公式;
(2)设bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA、OB是两条公路(近似看成两条直线), ![]() ,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N.
,在∠AOB内有一纪念塔P(大小忽略不计),已知P到直线OA、OB的距离分别为PD、PE,PD=6千米,PE=12千米.现经过纪念塔P修建一条直线型小路,与两条公路OA、OB分别交于点M、N. 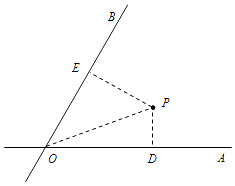
(1)求纪念塔P到两条公路交点O处的距离;
(2)若纪念塔P为小路MN的中点,求小路MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在(﹣1,+∞)是增函数.
在(﹣1,+∞)是增函数.
(1)当b=1时,求a的取值范围.
(2)若g(x)=f(x)﹣1008没有零点,f(1)=0,求f(﹣3)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com