
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,对
,对![]() 不成立,从而可得数列
不成立,从而可得数列![]() 的通项公式;(2)当
的通项公式;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() ,利用裂项相消法可得
,利用裂项相消法可得![]() ,再验证
,再验证![]() 时,是否成立即可.
时,是否成立即可.
试题解析:(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
对![]() 不成立,
不成立,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]()
所以![]()
![]()
又![]() 时,
时,![]() 符合上式,
符合上式,
所以![]() (
(![]() ).
).
【方法点晴】本题主要考查数列的通项公式与求和,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1)![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
![]() ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,边a、b、c分别是角A、B、C的对边,且满足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面积为4![]() ,b=4
,b=4![]() ,求△ABC的周长
,求△ABC的周长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:

(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是首项
是首项![]() 的等差数列,设
的等差数列,设![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,记![]() ,若对任意正整数
,若对任意正整数![]() ,不等式
,不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为2米的水轮如图所示,水轮圆心![]() 距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点
距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.
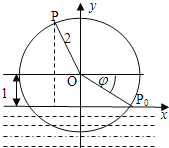
(1)试将点![]() 距离水面的高度
距离水面的高度![]() (单位:米)表示为时间
(单位:米)表示为时间![]() (单位:秒)的函数
(单位:秒)的函数![]() ;
;
(2)点![]() 第一次到达最高点大约要多长时间?
第一次到达最高点大约要多长时间?
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】伴随着智能手机的深入普及,支付形式日渐多样化,打破了传统支付的局限性和壁垒,有研究表明手机支付的使用比例与人的年龄存在一定的关系,某调研机构随机抽取了50人,对他们一个月内使用手机支付的情况进行了统计,如下表:

(1)若以“年龄55岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用手机支付”与人的年龄有关;
的把握认为“使用手机支付”与人的年龄有关;

(2)若从年龄在![]() ,
,![]() 内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为
内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为![]() .
.
①求随机变量![]() 的分布列;
的分布列;
②求随机变量![]() 的数学期望.
的数学期望.
参考数据如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影为点
上的正投影为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
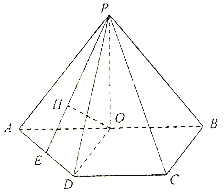
(1)求证:![]() 为
为![]() 中点;
中点;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的2倍,且过点
的长轴长是短轴长的2倍,且过点![]() .
.
⑴求椭圆![]() 的方程;
的方程;
⑵若在椭圆上有相异的两点![]() (
(![]() 三点不共线),
三点不共线),![]() 为坐标原点,且直线
为坐标原点,且直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() .
.
(ⅰ)求证: ![]() 是定值;
是定值;
(ⅱ)设![]() 的面积为
的面积为![]() ,当
,当![]() 取得最大值时,求直线
取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com