
| 车间 | 每辆童车所需的加工工时 | 有效工时(小时/日) | |
| A | B | ||
| 机械 | 0.8 | 1.2 | 40 |
| 油漆 | 0.6 | 0.8 | 30 |
| 装配 | 0.4 | 0.6 | 25 |
| 利润(元/辆) | 6 | 10 | |
分析 设x,y(单位辆)分别是A,B两种型号童车的日生产量,工厂每日可获得利润为z元,写出约束条件、目标函数,欲求利润最大,即求可行域中的最优解,在线性规划的解答题中使用直线平移法求出最优解,即将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.注意:最后要将所求最优解还原为实际问题.
解答 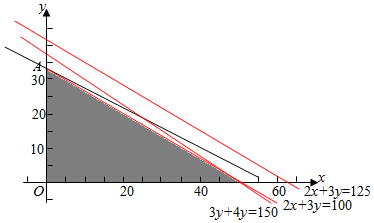 解:设x,y(单位辆)分别是A,B两种型号童车的日生产量,工厂每日可获得利润为z元,则z=6x+10y,其中x,y满足约束条件:…(1分)
解:设x,y(单位辆)分别是A,B两种型号童车的日生产量,工厂每日可获得利润为z元,则z=6x+10y,其中x,y满足约束条件:…(1分)
$\left\{\begin{array}{l}{0.8x+1.2y≤40}\\{0.6x+0.8y≤30}\\{0.4x+0.6y≤25}\\{x,y∈N}\end{array}\right.$,即$\left\{\begin{array}{l}{2x+3y≤100}\\{3x+4y≤150}\\{2x+3y≤125}\\{x,y∈N}\end{array}\right.$,…(4分)
作出可行域如图:
…(7分)
将z=6x+10y化成直线l:y=-$\frac{3}{5}$x+$\frac{1}{10}$z,当z变化时,直线l的斜率为-$\frac{3}{5}$,在y轴上的截距为$\frac{1}{10}$z的一簇平行直线,
当直线在y轴上的截距最大时z取最大值.
由图易知,直线过A点时,z取最大值,
由$\left\{\begin{array}{l}{x=0}\\{2x+3y=100}\end{array}\right.$得A(0,$\frac{100}{3}$)…(9分)
由于A点不是整数点,在可行域的整数点中,(2,32)是最优解.
此时zmax=322(元)…(11分)
答:生产A种童车2辆,B种童车32辆,能使工厂获得最大利润,最大利润为332元.…(12分)
点评 在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
圆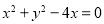 的圆心坐标和半径分别为( )
的圆心坐标和半径分别为( )
A.(0,2),2 B.(2,0),2 C.(-2,0),4 D.(2,0),4
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{3},\frac{π}{2})$ | B. | $(\frac{π}{3},π)$ | C. | $(\frac{π}{3},\frac{4π}{3})$ | D. | $(\frac{π}{3},\frac{2π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com