
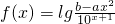 ,函数y=f(x)与函数y=g(x)满足如下对应关系:当点(x,y)在y=f(x)的图象上时,点
,函数y=f(x)与函数y=g(x)满足如下对应关系:当点(x,y)在y=f(x)的图象上时,点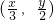 在y=g(x)的图象上,且f(0)=0,g(-1)=1.
在y=g(x)的图象上,且f(0)=0,g(-1)=1.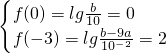 ,解得
,解得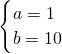 ,
,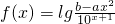 =
=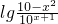 ,x∈(
,x∈( ,
, )
)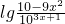 ,即y=
,即y=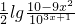 ,
,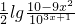 ;
; ,0),
,0), ,0),且x1<x2,
,0),且x1<x2, ,0)上单调递增,
,0)上单调递增,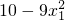 )-(
)-(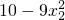 )
) ,0),且x1<x2,
,0),且x1<x2, ,0),
,0), ,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间(
,0),由复合函数的单调性,只需证明函数m(x)=10-9x2在区间( ,0)上单调递增即可,由单调性的定义可证.
,0)上单调递增即可,由单调性的定义可证.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com