
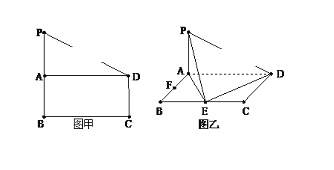
【题目】如图甲,在直角梯形PBCD中,PB∥CD,CD⊥BC,BC=PB=2CD,A是PB的中点.
现沿AD把平面PAD折起,使得PA⊥AB(如图乙所示),E、F分别为BC、AB边的中点.
(1)求证:平面PAE⊥平面PDE;
(2)在PE上找一点Q,使得平面BDQ⊥平面ABCD.
(3)在PA上找一点G,使得FG∥平面PDE.
【答案】(1)见解析; (2)当PQ=2QE时,平面BDQ⊥平面ABCD; (3)满足AG=![]() AP时,有FG∥平面PDE..
AP时,有FG∥平面PDE..
【解析】
(1)现根据线面平行的判定得到PA⊥平面ABCD,根据底面图形特点得到AE⊥ED,又因为PA⊥ED进而得到ED⊥平面PAE,可推得面面垂直;(2)假设平面BDQ⊥平面ABCD,面BDQ交底面ABCD于H点,根据线面平行的性质得到PA平行于面BDQ,QH平行于PA再由相似导出比例关系;(3)过点F作FH∥ED交AD于H,再过H作GH∥PD交PA于G,连接FG,证明平面FHG∥平面PED,即可证明FG∥平面PDE.
(1)证明:因为PA⊥AD, PA⊥AB, AB![]() AD=A,
AD=A,
所以PA⊥平面ABCD.因为BC=PB=2CD, A是PB的中点,所以ABCD是矩形,
又E为BC边的中点,所以AE⊥ED.
又由PA⊥平面ABCD, 得PA⊥ED, 且PA![]() AE=A, 所以ED⊥平面PAE,
AE=A, 所以ED⊥平面PAE,
而ED![]() 平面PDE,故平面PAE⊥平面PDE.
平面PDE,故平面PAE⊥平面PDE.
(2)假设平面BDQ⊥平面ABCD,面BDQ交底面ABCD于H点,又因为由第一问得到PA⊥平面ABCD,可得到直线PA平行于面BDQ,由线面平行的性质得到QH平行于PA,因为AD平行于BE,BE:AD=EH:HA=1:2,根据三角形EHQ相似于三角形PAE,故得到EQ:EP=HQ:AP=2:3.故当PQ=2QE时,平面BDQ⊥平面ABCD.
(3)过点F作FH∥ED交AD于H,再过H作GH∥PD交PA于G, 连结FG.

由FH∥ED, ED![]() 平面PED, 得FH∥平面PED;
平面PED, 得FH∥平面PED;
由GH∥PD,PD![]() 平面PED,得GH∥平面PED,
平面PED,得GH∥平面PED,
又FH![]() GH=H,所以平面FHG∥平面PED.所以FG∥平面PDE.
GH=H,所以平面FHG∥平面PED.所以FG∥平面PDE.
再分别取AD、PA的中点M、N,连结BM、MN,
易知H是AM的中点,G是AN的中点,
从而当点G满足AG=![]() AP时,有FG∥平面PDE.
AP时,有FG∥平面PDE.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知2Sn=3n+1+2n﹣3.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一动圆与定圆![]() 外切,同时和圆
外切,同时和圆![]() 内切,定点A(1,1).
内切,定点A(1,1).
(1)求动圆圆心P的轨迹E的方程,并说明是何种曲线;
(2)M为E上任意一点, F为E的左焦点,试求![]() 的最小值;
的最小值;
(3)试求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
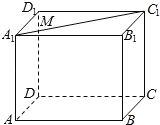
【题目】如图,在正方体![]() 中,若
中,若![]() 是线段
是线段![]() 上的动点,则下列结论不正确的是( )
上的动点,则下列结论不正确的是( )
A. 三棱锥![]() 的正视图面积是定值
的正视图面积是定值
B. 异面直线![]() ,
,![]() 所成的角可为
所成的角可为![]()
C. 异面直线![]() ,
,![]() 所成的角为
所成的角为![]()
D. 直线![]() 与平面
与平面![]() 所成的角可为
所成的角可为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() ,
,![]() 的直线倾斜角为
的直线倾斜角为![]() ,原点到该直线的距离为
,原点到该直线的距离为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)斜率大于零的直线过![]() 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若![]() ,求直线EF的方程.
,求直线EF的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是线段BF上一点,AB=AF=BC=2.
2CE,G是线段BF上一点,AB=AF=BC=2. 
(1)当GB=GF时,求证:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在点G满足BF⊥平面AEG?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com