
【题目】已知函数![]() ,其中
,其中![]() .
.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
![]() Ⅱ
Ⅱ![]() 设
设![]() 是定义在
是定义在![]() 上的函数,在
上的函数,在![]() 内任取
内任取![]() 个数
个数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() ,令
,令![]() ,
,![]() ,如果存在一个常数
,如果存在一个常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 在区间
在区间![]() 上的具有性质P.试判断函数
上的具有性质P.试判断函数![]() 在区间
在区间![]() 上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.
上是否具有性质P?若具有性质P,请求出M的最小值;若不具有性质P,请说明理由.![]() 注:
注:![]()
【答案】![]() Ⅰ
Ⅰ![]() ;
;![]() Ⅱ
Ⅱ![]() 具有,最小值为3
具有,最小值为3
【解析】
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 恒成立,可转化为
恒成立,可转化为![]() 恒成立,进而转化为函数最值问题解决;
恒成立,进而转化为函数最值问题解决;
![]() Ⅱ
Ⅱ![]() 先研究函数
先研究函数![]() 在区间
在区间![]() 上的单调性,然后对
上的单调性,然后对![]() 内的任意一个取数方法
内的任意一个取数方法![]() ,根据性质P的定义分两种情况讨论即可:①存在某一个整数
,根据性质P的定义分两种情况讨论即可:①存在某一个整数![]() 2,3,
2,3,![]() ,
,![]() ,使得
,使得![]() 时,②当对于任意的
时,②当对于任意的![]() 1,2,3,
1,2,3,![]() ,
,![]() ,
,![]() 时,
时,![]() ,利用函数的单调性去绝对值,化简,求
,利用函数的单调性去绝对值,化简,求![]() 的最小值.
的最小值.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 时,
时,![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以![]() ,即
,即![]() ,
,
所以![]() 即a的取值范围是
即a的取值范围是![]() .
.
![]() Ⅱ
Ⅱ![]() 由已知
由已知![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
对于![]() 内的任意一个取数方法
内的任意一个取数方法![]() ,
,
当存在某一个整数![]() 2,3,
2,3,![]() ,
,![]() ,使得
,使得![]() 时,
时,
![]()
![]()
![]()
![]() .
.
当对于任意的![]() 1,2,3,
1,2,3,![]() ,
,![]() ,
,![]() 时,则存在一个实数k使得
时,则存在一个实数k使得![]() ,
,
此时![]()
![]()
![]()
![]()
![]() ,
,![]()
当![]() 时,
时,![]() 式
式![]() ,
,
当![]() 时,
时,![]() 式
式![]() ,
,
当![]() 时,
时,![]() 式
式![]() .
.
综上,对于![]() 内的任意一个取数方法
内的任意一个取数方法![]() ,均有
,均有![]() .
.
所以存在常数![]() ,使
,使![]() 恒成立,
恒成立,
所以函数![]() 在区间
在区间![]() 上具有性质P.
上具有性质P.
此时M的最小值为3.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】如图,MN分别是边长为1的正方形ABCD的边BCCD的中点,将正方形沿对角线AC折起,使点D不在平面ABC内,则在翻折过程中,有以下结论:
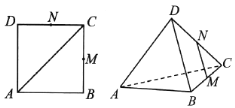
①异面直线AC与BD所成的角为定值.
②存在某个位置,使得直线AD与直线BC垂直.
③存在某个位置,使得直线MN与平面ABC所成的角为45°.
④三棱锥M-ACN体积的最大值为![]() .
.
以上所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地空气中出现污染,须喷洒一定量的去污剂进行处理.据测算,每喷洒1个单位的去污剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
,若多次喷洒,则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知,当空气中去污剂的浓度不低于4(毫克/立方米)时,它才能起到去污作用.
(Ⅰ)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(Ⅱ)若第一次喷洒2个单位的去污剂,6天后再喷洒![]()
![]() 个单位的去污剂,要使接下来的4天中能够持续有效去污,试求
个单位的去污剂,要使接下来的4天中能够持续有效去污,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学应用知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
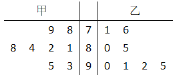
(Ⅰ)分别估计甲、乙两名同学在培训期间所有测试成绩的平均分;
(Ⅱ)从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考,求甲、乙两人成绩都在90分以上的概率;
(Ⅲ)现要从甲、乙中选派一人参加正式比赛,根据所抽取的两组数据分析,你认为选派哪位同学参加较为合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax2-x.
(Ⅰ)讨论f(x)在[0,+∞)上的单调性;
(Ⅱ)若函数g(x)=f(x)+x有两个极值点x1,x2,且x1<x2,求证:g(x2)>![]() -ln2.
-ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边过点P(-2,-1).
(1)求cos(2α+![]() )的值;
)的值;
(2)若角β满足tanβ=2,求tan(2α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】开发商现有四栋楼A,B,C,D.楼D位于BC间,到楼A,B,C的距离分别为![]() ,
,![]() ,
,![]() ,且从楼D看楼A,B的视角为
,且从楼D看楼A,B的视角为![]() .如图所示,不计楼大小和高度.
.如图所示,不计楼大小和高度.
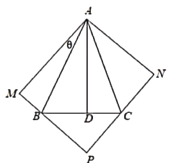
(1)试求从楼A看楼B,C视角大小;
(2)开发商为谋求更大开发区域,拟再建三栋楼M,P,N,形成以楼AMPN为顶点的矩形开发区域,规划要求楼B,C分别位于楼MP和楼PN间,如图所示,记![]() ,当
,当![]() 等于多少时,矩形开发区域面积最大?
等于多少时,矩形开发区域面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要建造一段![]() 长的高速公路,工程队需要把380名施工人员分为两组,一组负责
长的高速公路,工程队需要把380名施工人员分为两组,一组负责![]() 的软土地带的施工,另一组完成剩下的
的软土地带的施工,另一组完成剩下的![]() 硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
硬土地带的施工.根据工程技术人员的测算,软、硬地带每米公路的工程量分别为50人·天和30人·天.
(1)设参与软土地带工作的人数为![]() 人,试分别写出在软、硬地带筑路的时间
人,试分别写出在软、硬地带筑路的时间![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)问如何安排两组的人数,才能使全队筑路工期最短?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com