4
分析:
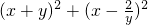
表示(x,x)与(-y,

)两点距离的平方,相应动点的轨迹为直线y=x,曲线y=-

,求出与直线y=x平行,且与曲线y=-

相切的直线方程,则切点到直线的距离的平方为所求.
解答:
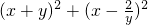
表示(x,x)与(-y,

)两点距离的平方,相应动点的轨迹为直线y=x,曲线y=-

求出与直线y=x平行,且与曲线y=-

相切的直线方程,则切点到直线的距离的平方为所求.
由y=-

可得
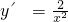
,令
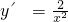
=1,则x=

,故可得切点的坐标为
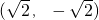
,

由点到直线的距离公式可得
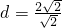
=2
∴
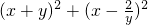
的最小值为4
故答案为:4
点评:本题考查两点间距离公式的运用,考查导数的几何意义,考查学生分析解决问题的能力.

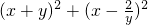 的最小值为________.
的最小值为________.