
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面ADE.
【答案】
(1)证明:建立如图所示的空间直角坐标系D﹣xyz,
不妨设正方体的棱长为2,则A(2,0,0),E(2,2,1),
F(0,1,0),A1(2,0,2),D1(0,0,2),
设平面AED的法向量为
![]() =(x1,y1,z1),
=(x1,y1,z1),
则 ![]() =(x1,y1,z1)(2,0,0)=0,
=(x1,y1,z1)(2,0,0)=0,
![]() =(x1,y1,z1)(2,2,1)=0,
=(x1,y1,z1)(2,2,1)=0,
∴2x1=0,2x1+2y1+z1=0.
令y1=1,得 ![]() =(0,1,﹣2),
=(0,1,﹣2),
同理可得平面A1FD1的法向量 ![]() =(0,2,1).
=(0,2,1).
∵ ![]() =0,∴
=0,∴ ![]() ,
,
∴平面AED⊥平面A1FD1.

(2)解:由于点M在直线AE上,
设 ![]() =λ(0,2,1)=(0,2λ,λ).
=λ(0,2,1)=(0,2λ,λ).
可得M(2,2λ,λ),∴ ![]() =(0,2λ,λ﹣2),
=(0,2λ,λ﹣2),
∵AD⊥A1M,∴要使A1M⊥平面ADE,
只需A1M⊥AE,
∴ ![]() =(0,2λ,λ﹣2)(0,2,1)=5λ﹣2=0,
=(0,2λ,λ﹣2)(0,2,1)=5λ﹣2=0,
解得λ= ![]() .故当A=
.故当A= ![]() A时,A1M⊥平面ADE
A时,A1M⊥平面ADE
【解析】(1)建立如图所示的空间直角坐标系D﹣xyz,不妨设正方体的棱长为2,设平面AED的法向量为 ![]() =(x1,y1,z1),
=(x1,y1,z1),
利用 ![]() =0,
=0, ![]() =0,得
=0,得 ![]() =(0,1,﹣2),同理可得平面A1FD1的法向量
=(0,1,﹣2),同理可得平面A1FD1的法向量 ![]() =(0,2,1).
=(0,2,1).
通过 ![]() =0,证明平面AED⊥平面A1FD1.(2)由于点M在直线AE上,设
=0,证明平面AED⊥平面A1FD1.(2)由于点M在直线AE上,设 ![]() =(0,2λ,λ).
=(0,2λ,λ). ![]() =(0,2λ,λ﹣2),利用AD⊥A1M,
=(0,2λ,λ﹣2),利用AD⊥A1M, ![]() =0,推出5λ﹣2=0,
=0,推出5λ﹣2=0,
解得λ= ![]() .故当A=
.故当A= ![]() A时,A1M⊥平面ADE点M在直线AE上,
A时,A1M⊥平面ADE点M在直线AE上,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为![]() =
=![]() (单位:万元),其中
(单位:万元),其中![]() 是产品售出的数量(单位:百件).
是产品售出的数量(单位:百件).
(1)该公司这种产品的年产量为![]() 百件,生产并销售这种产品所得到的利润为当年产量
百件,生产并销售这种产品所得到的利润为当年产量![]() 的函数
的函数![]() ,求
,求![]() ;
;
(2)当年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

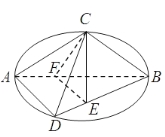
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人独立地对某一技术难题进行攻关.甲能攻克的概率为 ![]() ,乙能攻克的概率为
,乙能攻克的概率为 ![]() ,丙能攻克的概率为
,丙能攻克的概率为 ![]() .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励a万元.奖励规则如下:若只有1人攻克,则此人获得全部奖金a万元;若只有2人攻克,则奖金奖给此二人,每人各得 ![]() 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得 ![]() 万元.设甲得到的奖金数为X,求X的分布列和数学期望.
万元.设甲得到的奖金数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当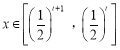 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若函数![]() ,
, ![]() 的最小值为-16,求实数
的最小值为-16,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上是单调减函数,求实数
上是单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com