
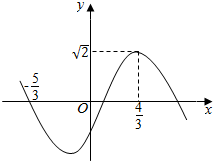
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.分析 (1)由已知得A=$\sqrt{2}$,T=$\frac{4}{3}(\frac{4}{3}+\frac{5}{3})$=4,从而ω=$\frac{2π}{4}$=$\frac{π}{2}$,再把($\frac{4}{3},\sqrt{2}$)代入,由-π<φ<π,结合图象,能求出f(x).
(2)由已知得$\sqrt{2}sin(\frac{π}{2}{x}_{0}-\frac{π}{6})=-\frac{\sqrt{10}}{5}$,利用正弦加法定理和同角三角函数关系式能求出f(x0+$\frac{1}{3}$).
解答 解:(1)由函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象,
得:A=$\sqrt{2}$,T=$\frac{4}{3}(\frac{4}{3}+\frac{5}{3})$=4,∴ω=$\frac{2π}{4}$=$\frac{π}{2}$,
∴f(x)=$\sqrt{2}sin(\frac{π}{2}x+φ)$,
把($\frac{4}{3},\sqrt{2}$)代入,得:$\sqrt{2}=\sqrt{2}sin(\frac{π}{2}×\frac{4}{3}+φ)$,
由-π<φ<π,结合图象解得,φ=-$\frac{π}{6}$.
∴f(x)=$\sqrt{2}sin(\frac{π}{2}x-\frac{π}{6})$.
(2)∵f(x0)=-$\frac{\sqrt{10}}{5}$,且x0∈(-$\frac{2}{3}$,$\frac{4}{3}$),
∴$\sqrt{2}sin(\frac{π}{2}{x}_{0}-\frac{π}{6})=-\frac{\sqrt{10}}{5}$,
∴$\sqrt{2}sin(\frac{π}{2}{x}_{0})cos\frac{π}{6}$-$\sqrt{2}cos(\frac{π}{2}{x}_{0})sin\frac{π}{6}$=$\frac{\sqrt{6}}{2}sin(\frac{π}{2}{x}_{0})-\frac{\sqrt{2}}{2}cos(\frac{π}{2}{x}_{0})$=-$\frac{\sqrt{10}}{5}$,
∴$\sqrt{3}sin(\frac{π}{2}{x}_{0})-cos(\frac{π}{2}{x}_{0})=-\frac{2\sqrt{5}}{5}$,
∴$\sqrt{3}sin(\frac{π}{2}{x}_{0})-\sqrt{1-(si{n}^{2}(\frac{π}{2}{x}_{0})}$=-$\frac{2\sqrt{5}}{5}$,
整理,得20sin2($\frac{π}{2}{x}_{0}$)+2$\sqrt{15}$sin($\frac{π}{2}{x}_{0}$)-1=0,
解得sin($\frac{π}{2}{x}_{0}$)=$\frac{-\sqrt{15}+\sqrt{35}}{20}$或sin($\frac{π}{2}{x}_{0}$)=$\frac{-\sqrt{15}-\sqrt{35}}{20}$,
∴f(x0+$\frac{1}{3}$)=$\sqrt{2}sin(\frac{π}{2}{x}_{0})$=$\frac{-\sqrt{15}+\sqrt{35}}{20}$或f(x0+$\frac{1}{3}$)=sin($\frac{π}{2}{x}_{0}$)=$\frac{-\sqrt{15}-\sqrt{35}}{20}$.
点评 本题考查三角函数解析式和三角函数值的求法,是中档题,解题时要认真审题,注意正弦加法定理和同角三角函数关系式的合理运用.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
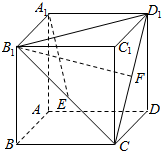 如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.
如图所示,正方体ABCD-A1B1C1D1中,E,F分别为侧面BB1C1C与CC1D1D的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在扇形AOB中,OA=OB=1,∠AOB=1弧度,圆C是扇形AOB的内切圆,圆C与OA切于T点.
如图在扇形AOB中,OA=OB=1,∠AOB=1弧度,圆C是扇形AOB的内切圆,圆C与OA切于T点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,5] | B. | [0,3] | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | [1,49] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com