
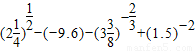 ;
; lg8+lg5•lg20+lg22.
lg8+lg5•lg20+lg22. 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2013 |
| 2 |
| 2013 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年大纲版高三上学期单元测试(4)数学试卷 题型:解答题
已知函数f(x)=A (A>0,
(A>0, >0,0<
>0,0< <
< ,且y=f(x)的最大值为2,其
,且y=f(x)的最大值为2,其
图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求 ;
;
(2)计算f (1) + f (2) +… + f ( 2 008 ).
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西南宁沛鸿民族中学高一下学期期中考试数学 题型:解答题
(本题满分12分)
已知函数f(x)=A (A>0,
(A>0,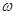 >0,0<
>0,0<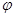 <
<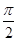 函数,且y=f (x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
函数,且y=f (x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求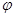 ;
;
(2)计算f(1)+f(2)+… +f(2 008).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年内蒙古乌兰察布市卓资县职业中学高一(上)期末数学复习试卷3(解析版) 题型:解答题
 ;
; lg8+lg5•lg20+lg22.
lg8+lg5•lg20+lg22.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com