
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 到点
到点![]() 的距离与
的距离与![]() 到直线
到直线![]() 的距离相等.
的距离相等.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设![]() 是曲线
是曲线![]() 上的点,点
上的点,点![]() 在曲线
在曲线![]() 上,直线
上,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】以下判断正确的是( )
A.函数y=f(x)为R上可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件
B.命题“存在x∈R,x2+x﹣1<0”的否定是“任意x∈R,x2+x﹣1>0”
C.命题“在锐角△ABC中,有 sinA>cosB”为真命题
D.“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设倾斜角为α的直线L: ![]() (T为参数)与曲线C:
(T为参数)与曲线C: ![]() (φ为参数)相交于不同的两点A,B.
(φ为参数)相交于不同的两点A,B.
(1)若α= ![]() ,若以坐标原点为极点,x轴的正半轴为极轴,求直线AB的极坐标方程;
,若以坐标原点为极点,x轴的正半轴为极轴,求直线AB的极坐标方程;
(2)若直线的斜率为 ![]() ,点P(2,
,点P(2, ![]() ),求|PA||PB|的值.
),求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
[145.5,149.5) | 1 | 0.02 |
[149.5,153.5) | 4 | 0.08 |
[153.5,157.5) | 20 | 0.40 |
[157.5,161.5) | 15 | 0.30 |
[161.5,165.5) | 8 | 0.16 |
[165.5,169.5) | m | n |
合 计 | M | N |

(1)求出表中![]() 所表示的数;
所表示的数;
(2)画出频率分布直方图;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:在棱![]() 上存在一点
上存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
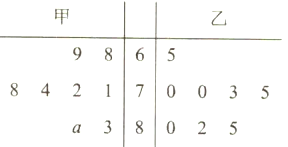
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com