
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:

(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
【答案】(1)![]() (2)96.8(3)
(2)96.8(3)![]()
【解析】
(1)由频率分布直方图的性质结合条件即可求解;
(2)每个小长方形底边中点所对应的横坐标乘以该组的频率,再求和即可求出平均数;
(3)用列举法先求出从抽取的5人中,随机抽取2人所包含的基本事件总数,以及抽取的这2人中其中一人成绩在![]() 分所包含的基本事件个数,结合古典概型的概率公式即可求出概率.
分所包含的基本事件个数,结合古典概型的概率公式即可求出概率.
(1)由条件及频率分别直方图的性质可知:![]()
解得![]()
(2)由(1)可知,成绩在![]() 分的有9人,在
分的有9人,在![]() 分的有24人,
分的有24人,
在![]() 分的有60人,在
分的有60人,在![]() 分的有45人,
分的有45人,
在![]() 分的有12人,故志愿者知识竞赛平均成绩为
分的有12人,故志愿者知识竞赛平均成绩为![]()
(3)由(2)可知,受奖励的15人中有三人的成绩是![]() 分,其余12人的成绩是
分,其余12人的成绩是![]() 分,利用分层抽样抽取5人,有1人成绩在
分,利用分层抽样抽取5人,有1人成绩在![]() 分中,4人成绩在
分中,4人成绩在![]() 分中.
分中.
记成绩是![]() 分的1人为
分的1人为![]() ,成绩是
,成绩是![]() 分的4人为
分的4人为![]() ,从这5人中抽取2人去主会场服务共有以下10种可能:
,从这5人中抽取2人去主会场服务共有以下10种可能:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
满足条件的有![]() ,
,![]() ,
,![]() ,
,![]() ,共4种,
,共4种,
故所求概率![]() .
.


科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.
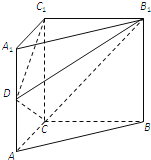
(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式:  ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1、F2,若椭圆C经过点(0,
(a>b>0)的左、右焦点分别为F1、F2,若椭圆C经过点(0,![]() ),离心率为
),离心率为![]() ,直线l过点F2与椭圆C交于A、B两点.
,直线l过点F2与椭圆C交于A、B两点.
(1)求椭圆C的方程;
(2)若点N为△F1AF2的内心(三角形三条内角平分线的交点),求△F1NF2与△F1AF2面积的比值;
(3)设点A,F2,B在直线x=4上的射影依次为点D,G, E.连结AE,BD,试问当直线l的倾斜角变化时,直线AE与BD是否相交于定点T?若是,请求出定点T的坐标;若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为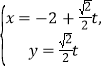 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|![]() ),x
),x![]() 为f(x)的零点,x
为f(x)的零点,x![]() 为y=f(x)图象的对称轴,且f(x)在(
为y=f(x)图象的对称轴,且f(x)在(![]() )上单调,则ω的最大值为_____.
)上单调,则ω的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com