
分析 (1)求导函数,利用曲线f(x)在点(1,f(1))处的切线斜率为-3,且x=2时,y=f(x)有极值,建立两个方程,即可求函数f(x)的解析式;
(2)确定函数的极值点,利用函数的最值在极值点处及端点处取得,即可得到结论.
解答 解:f′(x)=3x2+2ax+b,
(1)由题意,得f′(1)=3+2a+b=-3,f′(2)=12+4a+b=0,
解得a=-3,b=0,∴f(x)=x3-3x2+1;
(2)由(1)知,f′(x)=3x2-6x=0,解得x=0或x=2.
当-1<x<0时,f′(x)>0,f(x)在(-1,0)是增函数,
当0<x<1时,f′(x)<0,f(x)在(0,1)是减函数,
f(0)=1,f(1)=-1,f(-1)=-3,
∴f(x)在[-1,1]上的最大值为1,最小值为-3.
点评 本题考查了利用导数研究曲线上某点切线方程,考查导数知识的运用,考查导数的几何意义,考查函数的极值与最值,考查学生的计算能力,属于中档题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
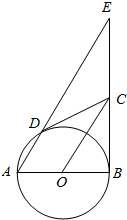 如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.
如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
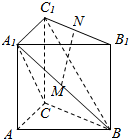 如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.
如图所示,在三棱柱ABC-A1B1C1中,∠ACB=90°,AA1⊥平面ABC,AC=BC=CC1,M,N分别为A1B,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
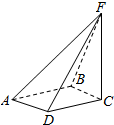 如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=$\sqrt{2}$.CF与平面 ABCD垂直,CF=2.求二面角B-AF-D的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com