
【题目】在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(1)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(2)从上表三个社区的志愿者中各任取1人调查情况,以X表示负责现场值班值守的人数,求X的分布列;
(3)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询满意,“
”分别表示A,B,C社区的人们对心理咨询满意,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询不满意,写出方差
”分别表示A,B,C社区的人们对心理咨询不满意,写出方差![]() ,
,![]() ,
,![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
【答案】(1)![]() (2)详见解析(3)
(2)详见解析(3)![]()
【解析】
(1)利用古典概型概率公式求解即可;
(2)先求出A,B,C三个社区负责现场值班值守的概率,得出X的所有可能取值,并计算出相应的概率,即可得出分布列;
(3)根据方差的意义进行判断即可.
解:(1)记“从上表三个社区的志愿者中任取1人,此人来自于A社区,并且参与社区消毒工作”为事件D,
![]() .
.
所以从上表三个社区的志愿者中任取1人,此人来自于A社区,并且参与社区消毒工作的概率为![]() .
.
(2)从上表三个社区的志愿者中各任取1人,由表可知:A,B,C三个社区负责现场值班值守的概率分别为![]() ,
,![]() ,
,![]() .
.
X的所有可能取值为0,1,2,3.
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(3)![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北爆发新型冠状病毒肺炎疫情以来,湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD,四边形ABCD是边长为3的正方形,平面![]() 平面
平面![]() ,
,![]() 于点O,
于点O,![]() ,点E在棱PB上,
,点E在棱PB上,![]() .
.
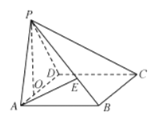
(1)当![]() 时,求直线AE与平面PCD所成角的正弦值;
时,求直线AE与平面PCD所成角的正弦值;
(2)若二面角B-PC-D的余弦值为![]() ,求PO的长.
,求PO的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)若以![]() 为直径的圆恰好经过椭圆右焦点
为直径的圆恰好经过椭圆右焦点![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
(2)求证:![]() 的内切圆的圆心在定直线
的内切圆的圆心在定直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
②函数![]() 的最小值为2
的最小值为2
③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
④已知双曲线![]() 过点
过点![]() ,且渐近线为
,且渐近线为![]() ,则离心率
,则离心率![]() ,其中所有正确命题的编号是:_______.
,其中所有正确命题的编号是:_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值;
(2)设函数g(x)=x3-6x+5,x∈R. 若关于x的方程g(x)=m有三个不同的实根,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com