Question

在平面直角坐标系xOy中，点P到点F（3，0）的距离的4倍与它到直线x=2的距离的3倍之和记为d，当P点运动时，d恒等于点P的横坐标与18之和
（Ⅰ）求点P的轨迹C；
（Ⅱ）设过点F的直线I与轨迹C相交于M，N两点，求线段MN长度的最大值．

Answer 1

分析：（1）由题意，要求动点的轨迹方程，由于已经告诉了动点所满足的约束条件所以利用直接法求其轨迹即可：
（2）由题意及解析式画出图形，利用直线与曲线的轨迹方程联立，通过图形讨论直线与轨迹的交点，利用两点间的距离公式求解即可．

解答：解（Ⅰ）设点P的坐标为（x，y），由题设则d=4

(x-3)2+y2

+3︳x-2︳①由题意轨迹图（1）如下：
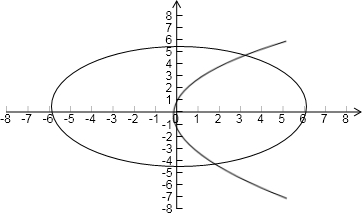
（图1）
当x＞2时，由①得

(x-3)2+y2

=6-

1

2

x，
化简得

x2

36

+

y2

27

=1．
当x≤2时由①得

(3-x)2+y2

=3+x
化简得y²=12x
故点P的轨迹C是椭圆C1：

x2

36

+

y2

27

=1在直线x=2的右侧
部分与抛物线C₂：y²=12x在直线
x=2的左侧部分（包括它与直线x=2
的交点）所组成的曲线，参见图1
（Ⅱ）如图2所示，
易知直线x=2与C₁，C₂的交点都是A（2，2

6

），
B（2，-2

6

），直线AF，BF的斜
率分别为k_AF=-2

6

，k_BF=2

6

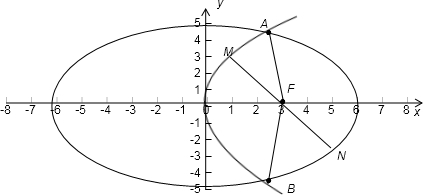
．                       图2
当点P在C₁上时，由②知|PF|=6-

1

2

x．④
当点P在C₂上时，由③知|PF|=3+x⑤
若直线l的斜率k存在，则直线l的方程为y=k（x-3）
（1）当k≤k_AF，或k≥k_BF，即k≤-2

6

时，直线I与轨迹C的两个交点M（x₁，y₁），N（x_，y_）都在C₁上，此时由④知
|MF|=6-

1

2

x₁|NF|=6-

1

2

x_
从而|MN|=|MF|+|NF|=（6-

1

2

x₁）+（6-

1

2

x_）=12-

1

2

（x₁+x_）
由

y=k(x-3) x2 36 + y2 27 =1

得（3+4k²）x²-24k²x+36k²-108=0则x₁，x是这个方程的两根，
所以x₁+x_=

24k2

3+4k2

*|MN|=12-

1

2

（x₁+x_）=12-

12k2

3+4k2

因为当k≤2

6

，或k≥2

6

时，k²≥24，|MN|=12-

12k2

3+4k2

=12-

12

1 k2 +4

=

100

11

．
当且仅当k=±2

6

时，等号成立．
（2）当kAE＜k＜kAN，-2

6

＜k＜2

6

时，直线L与轨迹C的两个交点M（x₁，y₁），N（x₂，y₂）分别在C₁，C₂上，不妨设点M在C₁上，点C₂上，则④⑤知，|MF|=6-

1

2

x1，|NF|=3+x2
设直线AF与椭圆C₁的另一交点为E（x₀，y₀），则x₀＜x₁，x₂＜2.|MF|=6-

1

2

x1＜6-

1

2

x0=|EF|，|NF|=3+x2＜3+2=|AF|
所以|MN|=|MF|+|NF|＜|EF|+|AF|=|AE|．而点A，E都在C₁上，且kAE=-2

6

，有（1）知|AE|=

100

11

，所以|MN|＜

100

11

若直线ι的斜率不存在，则x₁=x₂=3，此时|MN|=12-

1

2

(x1+x2)=9＜

100

11

综上所述，线段MN长度的最大值为

100

11

．

点评：（1）此问重点考查了直接法求动点的轨迹方程，还考查了对于含绝对值的式子化简时的讨论；
（2）此问重点考查了利用图形抓住题目中的信息，分类讨论的思想，还考查了圆锥曲线中的焦半径公式（用点的一个坐标表示），还考查了两点间的距离公式．