
����Ŀ��ij�ص�������ѧУ���������ʾ�����У�Ϊ���ƶ���ѧ�����߲�������һ����ʡʮ�ʡ����µĹ����ƶȣ��¹����ƶ�ʵʩһ��ʱ���ѧУ���¹����ƶ������ȡ����ѧ�������ʾ����飬���������10�����⣬ÿ������10�֣���������������ֳ�5�飺[50��60����60��70����[70��80����[80��90����[90��100]��������Ƶ�ʷֲ�ֱ��ͼ�����������ľ�Ҷͼ��ͼ�н��г��˵÷���[50��60����[90��100]�����ݣ��� 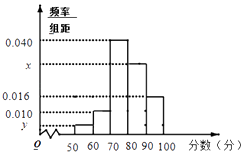
��1������������n��Ƶ�ʷֲ�ֱ��ͼ�е�x��y��ֵ��
��2����ѡȡ�������У��ӷ�����70�����µ�ѧ���������ȡ2��ѧ��������̸�ᣬ������ȡ��2��ѧ����ǡ��һ�˵÷���[50��60���ڵĸ��ʣ�
5 | 3 4 |
���𰸡�
��1���⣺�������֪����������n= ![]() =50��
=50��
y= ![]() =0.004��
=0.004��
x=0.100��0.004��0.010��0.016��0.040=0.030��
��2���⣺�������֪��������[60��70���ڵ�ѧ����5�ˣ�������[50��60���ڵ�ѧ����2�ˣ���ȡ��2��ѧ������������� ![]() =21�֣�����2��ͬѧ�ķ���ǡ��һ����[50��60���ڵ������10�֣�
=21�֣�����2��ͬѧ�ķ���ǡ��һ����[50��60���ڵ������10�֣�
������ȡ��2��ѧ����ǡ��һ�˵÷���[50��60���ڵĸ���P= ![]() ��
��
����������1��������������Ƶ��Ƶ�ʵĹ�ϵ�ô𰸣���2���������֪��������[60��70���ڵ�ѧ����5�ˣ�������[50��60���ڵ�ѧ����2�ˣ��������֪ʶ�ɵû����¼� �ĸ���������������ȡ��2��ѧ����ǡ��һ�˵÷���[50��60���ڵĸ��ʣ�
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���
�У���![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ��ֱ��
���������Ϊ���Ὠ��������ϵ��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ ������
������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1��д��ֱ��![]() ��ֱ�����귽�̺�����
��ֱ�����귽�̺�����![]() ����ͨ���̣�
����ͨ���̣�
��2����ֱ��![]() ������
������![]() �Ľ����ֱ������.
�Ľ����ֱ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǿ���dz�������Ϊ��������������֣�����ͨ6������˽�ҳ�Ͷ����ǿ�յ�һ��ķ��ã������ѣ�ͳһΪ![]() Ԫ������һ������ʱ��ʵ�е��Ƿ��ʸ������ƣ���������һ��ȳ���������·��ͨ�¹ʵ��������ϵ��������ͨ�¹ʵĴ���Խ�࣬����Ҳ��Խ�ߣ����帡����������
Ԫ������һ������ʱ��ʵ�е��Ƿ��ʸ������ƣ���������һ��ȳ���������·��ͨ�¹ʵ��������ϵ��������ͨ�¹ʵĴ���Խ�࣬����Ҳ��Խ�ߣ����帡����������
��ǿ�ո������غ������ʱ��ʱ� | ||
�������� | �������� | |
| ��һ�����δ���������ε�·��ͨ�¹� | �¸�10% |
| ���������δ���������ε�·��ͨ�¹� | �¸�20% |
| ���������������δ���������ε�·��ͨ�¹� | �¸�30% |
| ��һ����ȷ���һ�������β��漰�����ĵ�·��ͨ�¹� | 0% |
| ��һ����ȷ������μ��������������ε�·��ͨ�¹� | �ϸ�10% |
| ��һ����ȷ��������ε�·��ͨ�����¹� | �ϸ�30% |
ij����Ϊ���о�ijһƷ����ͨ6������˽�ҳ���Ͷ������������ȡ��60��������������ĸ�Ʒ��ͬ�ͺ�˽�ҳ�����һ������ʱ�������ͳ�Ƶõ�������ı���
���� |
|
|
|
|
|
|
���� | 10 | 5 | 5 | 20 | 15 | 5 |
����60����Ʒ�Ƴ���Ͷ�����͵�Ƶ�ʴ���һ����Ͷ�����͵ĸ��ʣ�����������⣺
![]() �����ҹ�����������ͨ�¹�����ǿ�Ʊ���������������ǿ�ռ۸�Ĺ涨��
�����ҹ�����������ͨ�¹�����ǿ�Ʊ���������������ǿ�ռ۸�Ĺ涨�� ![]() .ijͬѧ������һ����Ʒ�Ƴ��ҳ���������꣬��
.ijͬѧ������һ����Ʒ�Ƴ��ҳ���������꣬��![]() Ϊ��Ʒ�Ƴ��ڵ���������ʱ�ķ��ã���
Ϊ��Ʒ�Ƴ��ڵ���������ʱ�ķ��ã���![]() �ķֲ�������ѧ����ֵ������ѧ����ֵ��������λ���֣�
�ķֲ�������ѧ����ֵ������ѧ����ֵ��������λ���֣�
![]() ij���ֳ�������ר��������һƷ�ƵĶ��ֳ����ҽ���һ��Ľ�ǿ�ձ��Ѹ��ڻ������ѵij�����Ϊ�¹ʳ�.���蹺��һ���¹ʳ�����5000Ԫ��һ�����¹ʳ�ӯ��10000Ԫ��
ij���ֳ�������ר��������һƷ�ƵĶ��ֳ����ҽ���һ��Ľ�ǿ�ձ��Ѹ��ڻ������ѵij�����Ϊ�¹ʳ�.���蹺��һ���¹ʳ�����5000Ԫ��һ�����¹ʳ�ӯ��10000Ԫ��
�����������̹��������������������꣩��Ʒ�ƶ��ֳ���������������������һ���¹ʳ��ĸ��ʣ�
������������һ�ι���100���������������꣩��Ʒ�ƶ��ֳ�������������������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪n��N* �� ��Sn�ǵ����ݼ��ĵȱ�����{an}��ǰn��ͣ�a1= ![]() ��S2+a2 �� S4+a4 �� S3+a3�ɵȲ����У�
��S2+a2 �� S4+a4 �� S3+a3�ɵȲ����У�
��1��������{an}��ͨ�ʽ��
��2��������{nan}��ǰn���ΪTn �� ��֤����������������n�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ��x��3��2+��y��3��2=8���У�����x��y���Ͻؾ���ȵ�ֱ���У� ��
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() �ĵ������䣻
�ĵ������䣻
��2��������![]() ����һ����Сֵ����һ������ֵ����
����һ����Сֵ����һ������ֵ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() ��ʹ�õ�
��ʹ�õ�![]() ʱ��
ʱ�� ![]() ��ֵ����
��ֵ����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ![]() �У���Բ
�У���Բ![]() ��
�� ![]() ��
��![]() ������������
������������![]() ��������
��������![]() ��
�� ![]() �Ľ���
�Ľ���![]() ��
��![]() ��һ�����㣮
��һ�����㣮
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() ��
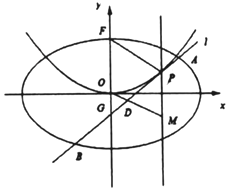
��![]() �϶��㣬��λ�ڵ�һ���ޣ�
�϶��㣬��λ�ڵ�һ���ޣ� ![]() �ڵ�
�ڵ�![]() ��������
��������![]() ��
��![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
�� ![]() ���߶�
���߶�![]() ���е�Ϊ
���е�Ϊ![]() ��ֱ��
��ֱ��![]() ���
���![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ���ֱ�߽��ڵ�
���ֱ�߽��ڵ�![]() ��
��
��i����֤����![]() �ڶ�ֱ���ϣ�
�ڶ�ֱ���ϣ�
��ii��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
�� ![]() �����Ϊ
�����Ϊ![]() ����
����![]() �����ֵ��ȡ�����ֵʱ��
�����ֵ��ȡ�����ֵʱ��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com