
�ɱ��ǹ�ʽ![]() ����֪cos2x���Ա�ʾΪcosx�Ķ��ζ���ʽ��
����֪cos2x���Ա�ʾΪcosx�Ķ��ζ���ʽ��
����cos3x��������![]()
![]()
![]()
![]()
�ɼ�cos3x���Ա�ʾΪcosx�����ζ���ʽ��һ��أ�����һ��n�ζ���ʽPn(t)��ʹ��![]() ����Щ����ʽPn(t)��Ϊ�б�ѩ�����ʽ��
����Щ����ʽPn(t)��Ϊ�б�ѩ�����ʽ��
(��)��֤��sin3x��3sinx��4sin3x��
(��)�����P4(t)������һ��cosx���Ĵζ���ʽ����ʾcos4x��
(��)���ý���![]()
![]() �����sin18���ֵ��
�����sin18���ֵ��
 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011����ʡ������Э�����һ4���¿���ѧ���� ���ͣ������
������С������12�֣�
�ɱ��ǹ�ʽ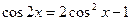 ����֪
����֪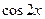 ���Ա�ʾΪ
���Ա�ʾΪ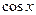 �Ķ��ζ���ʽ.
�Ķ��ζ���ʽ.
����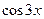 ��������
��������

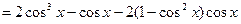

�ɼ�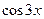 ���Ա�ʾΪ
���Ա�ʾΪ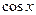 �����ζ���ʽ��һ��أ�����һ��
�����ζ���ʽ��һ��أ�����һ��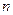 �ζ���ʽ
�ζ���ʽ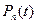 ��ʹ��
��ʹ��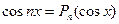 ����Щ����ʽ
����Щ����ʽ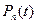 ��Ϊ�б�ѩ�����ʽ.
��Ϊ�б�ѩ�����ʽ.
��I����֤�� ��
��
��II������� ������һ��
������һ��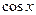 ���Ĵζ���ʽ����ʾ
���Ĵζ���ʽ����ʾ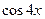 ��
��
(III)���ý���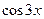
 �����
����� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011����ʡ������Э�����һ4���¿���ѧ���� ���ͣ������
������С������12�֣�
�ɱ��ǹ�ʽ ����֪
����֪ ���Ա�ʾΪ
���Ա�ʾΪ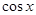 �Ķ��ζ���ʽ.
�Ķ��ζ���ʽ.
���� ��������
��������

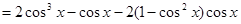

�ɼ� ���Ա�ʾΪ
���Ա�ʾΪ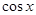 �����ζ���ʽ��һ��أ�����һ��
�����ζ���ʽ��һ��أ�����һ��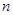 �ζ���ʽ
�ζ���ʽ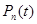 ��ʹ��
��ʹ�� ����Щ����ʽ
����Щ����ʽ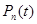 ��Ϊ�б�ѩ�����ʽ.
��Ϊ�б�ѩ�����ʽ.
��I����֤�� ��
��
��II�������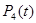 ������һ��
������һ��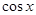 ���Ĵζ���ʽ����ʾ
���Ĵζ���ʽ����ʾ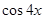 ��
��
(III)���ý���
 �����
����� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com