
【题目】已知△ABC中,三边长a,b,c满足a2﹣a﹣2b﹣2c=0,a+2b﹣2c+3=0,则这个三角形最大角的大小为_____.
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】某企业生产A产品的质量以其质量指标值衡量,质量指标值划分等级及产品售价如下表:
质量指标值m |
|
|
|
产品等级 | 等品 | 二等品 | 三等品 |
售价(每件) | 160元 | 140元 | 120元 |
从该企业生产的A产品中抽取100件作为样本,检测其质量指标值,得到下图的频率分布直方图.
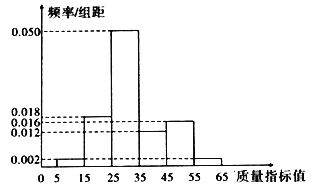
(1)根据频率分布直方图,求A产品质量指标值的中位数;
(2)用样本频率估计总体概率.现有一名顾客随机购买两件A产品,设其支付的费用为X元,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意的
对任意的![]() ,都有
,都有![]()
![]() ,且
,且![]() ,则称数列
,则称数列![]() 为“k级创新数列”.
为“k级创新数列”.
(1)已知数列![]() 满足
满足![]() 且
且![]() ,试判断数列
,试判断数列![]() 是否为“2级创新数列”,并说明理由;
是否为“2级创新数列”,并说明理由;
(2)已知正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,若
,若![]() ,求数列
,求数列![]() 的前n项积
的前n项积![]() ;
;
(3)设![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,令
,令![]() ,在(2)的条件下,记数列
,在(2)的条件下,记数列![]() 的通项
的通项![]() ,求证:
,求证:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() ,设
,设![]() 的内切圆分别与边
的内切圆分别与边![]() 相切于点
相切于点![]() ,已知
,已知![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与曲线E交于点
,与曲线E交于点![]() 轴,过
轴,过![]() 的另一直线与曲线
的另一直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1、F2在坐标轴上,焦距是实轴长的![]() 倍且过点(4,﹣
倍且过点(4,﹣![]() )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)在(2)条件下,若M F2交双曲线另一点N,求△F1MN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(1)为东方体育中心,其设计方案侧面的外轮廓线如图(2)所示;曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() 且
且![]() 恰好等于圆
恰好等于圆![]() 的半径,
的半径,![]() 与圆相切且
与圆相切且![]() .
.
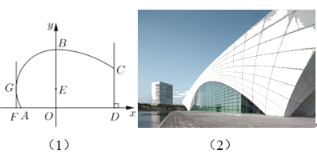
(1)若要求![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)当![]() 时,若要求
时,若要求![]() 不超过45米,求
不超过45米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com