
已知R上的不间断函数g(x)满足:①当x>0时,![]() (x)>0恒成立;②对任意的x∈R都有g(x)=g(-x).又函数f(x)满足:对任意的x∈R,都有f(
(x)>0恒成立;②对任意的x∈R都有g(x)=g(-x).又函数f(x)满足:对任意的x∈R,都有f(![]() +x)=-f(x)成立,当x∈[0,
+x)=-f(x)成立,当x∈[0,![]() ]时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤(a2-a+2)对x∈[-3,3]恒成立,则a的取值范围
]时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤(a2-a+2)对x∈[-3,3]恒成立,则a的取值范围
a≤0或a≥1
0≤a≤1
-1≤a≤1
a∈R
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知R上的不间断函数![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②对任意的
恒成立;②对任意的![]() 都有
都有![]() .又函数
.又函数![]() 满足:对任意的
满足:对任意的![]() ,都有
,都有![]() 成立,当
成立,当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围_______________.
的取值范围_______________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市高三上学期期末模拟文科数学试卷(解析版) 题型:选择题
已知R上的不间断函数 满足:①当
满足:①当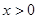 时,
时,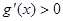 恒成立;②对任意的
恒成立;②对任意的 都有
都有 。又函数
。又函数 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当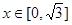 时,
时, 。若关于
。若关于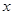 的不等式
的不等式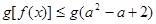 对
对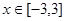 恒成立,则
恒成立,则 的取值范围( )
的取值范围( )
A.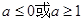 B.
B. C.
C. D.
D.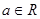
查看答案和解析>>
科目:高中数学 来源:2013届湖北长阳自治县第一中学高二下学期期中理科数学试卷(解析版) 题型:选择题
已知R上的不间断函数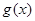 满足:①当
满足:①当 时,
时, 恒成立;②对任意的
恒成立;②对任意的 都有
都有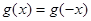 。又函数
。又函数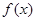 满足:对任意的
满足:对任意的 ,都有
,都有 成立,当
成立,当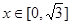 时,
时,
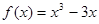 。若关于
。若关于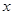 的不等式
的不等式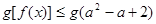 对
对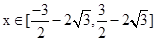 恒成立,则
恒成立,则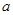 的取值范围( )
的取值范围( )
A. B.
B.  C.
C.
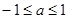 D.
D.
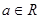
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com