
【题目】已知函数f(x)=![]() x2-aln x(a∈R).
x2-aln x(a∈R).
(1)若f(x)在x=2处取得极值,求a的值;
(2)求f(x)的单调区间;
(3)求证:当x>1时, ![]() x2+ln x<
x2+ln x<![]() x3.
x3.
【答案】(1)a=4;(2)见解析.;(3)见解析.
【解析】
(1)由f′(2)=0即可求出a=4。
(2)由题可得f(x)的定义域为x>0。求出f′(x) =x-![]() ,当a≤0时f′(x) >0恒成立。故f(x)在 (0,+∞) 单调递增;当a>0时,令f′(x)>0解得即为f(x)的单调増区间,令f′(x)<0解得即为f(x)的单调减区间。
,当a≤0时f′(x) >0恒成立。故f(x)在 (0,+∞) 单调递增;当a>0时,令f′(x)>0解得即为f(x)的单调増区间,令f′(x)<0解得即为f(x)的单调减区间。
(3)构造函数g(x)=![]() x3-
x3-![]() x2-ln x,利用导数得出g(x)在(1,+∞)上为单调递增。易得g(x) >0恒成立,进而可得到结论。
x2-ln x,利用导数得出g(x)在(1,+∞)上为单调递增。易得g(x) >0恒成立,进而可得到结论。
(1)解:f′(x)=x- ![]() ,因为x=2是一个极值点,
,因为x=2是一个极值点,
所以2-![]() =0,所以a=4.
=0,所以a=4.
(2)解:因为f′(x)=x-![]() ,f(x)的定义域为x>0,
,f(x)的定义域为x>0,
所以当a≤0时,f(x)的单调递增区间为(0,+∞).
当a>0时,f′(x)=x-![]() =
=![]() =
=![]() ,
,
令f′(x)>0,得x>![]() ,
,
所以函数f(x)的单调递增区间为(![]() ,+∞);
,+∞);
令f′(x)<0,得0<x<![]() ,
,
所以函数f(x)的单调递减区间为(0,![]() ).
).
(3)证明:设g(x)=![]() x3-
x3-![]() x2-ln x,
x2-ln x,
则g′(x)=2x2-x-![]() ,
,
因为当x>1时,g′(x)=![]() >0,
>0,
所以g(x)在(1,+∞)上是增函数.
所以g(x)>g(1)=![]() >0.
>0.
所以当x>1时,![]() x2+ln x<
x2+ln x<![]() x3.
x3.


科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC.
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
X1 | 5% | 10% |
P | 0.8 | 0.2 |
X2 | 2% | 8% | 12% |
P | 0.2 | 0.5 | 0.3 |
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差V(Y1)、V(Y2);
(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 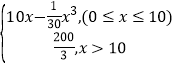 其中x(单位:万件)是年产量.
其中x(单位:万件)是年产量.
(1)写出年利润W(单位:万元)关于年产量x的函数解析式.
(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①线性回归方程![]() 至少经过点(x1,y1),(x2,y2),…,(xn ,yn)中的一个点;
至少经过点(x1,y1),(x2,y2),…,(xn ,yn)中的一个点;
②若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强;
之间的负相关很强;
③在回归分析中,相关指数![]() 为0.80的模型比相关指数
为0.80的模型比相关指数![]() 为0.98的模型拟合的效果要好;
为0.98的模型拟合的效果要好;
④在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是-7。
的值一定是-7。
其中假命题的个数是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句中是命题的有________,其中是真命题的有_____(填序号).
①“垂直于同一条直线的两个平面必平行吗?”②“一个数不是正数就是负数”;③“在一个三角形中,大角所对的边大于小角所对的边”;④“若x+y为有理数,则x,y都是有理数”;⑤作一个三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣2x,其中a≤0.
ax2﹣2x,其中a≤0.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+b,求a﹣2b的值;
(2)讨论函数f(x)的单调性;
(3)设函数g(x)=x2﹣3x+3,如果对于任意的x,t∈(0,1],都有f(x)≤g(t)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com