
【题目】已知函数![]() .
.
(1)当a=1时,求函数![]() 在(2,
在(2,![]() )处的切线方程:
)处的切线方程:
(2)当a=2时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(3)若![]() 在
在![]() 上是单调增函数,求实数a的取值范围.
上是单调增函数,求实数a的取值范围.
【答案】(2)![]() ; (2)
; (2)![]() 在
在![]() 上单调递增,f(x)无极值. (3)
上单调递增,f(x)无极值. (3)![]()
【解析】
(1)当![]() 时,求导函数,则函数在
时,求导函数,则函数在![]() 处的切线的斜率即为导数值
处的切线的斜率即为导数值![]() ,根据点斜式方程即可求出切线方程;
,根据点斜式方程即可求出切线方程;
(2)先求出函数的定义域,把![]() 代入到函数中并求出
代入到函数中并求出![]() 时
时![]() 的值,在定义域内讨论导函数的正负得到函数的单调区间及极值;
的值,在定义域内讨论导函数的正负得到函数的单调区间及极值;
(3)把![]() 代入到
代入到![]() 中得到
中得到![]() 的解析式,求出其导函数大于0即函数单调,可设
的解析式,求出其导函数大于0即函数单调,可设![]() ,求出其导函数在
,求出其导函数在![]() 上单调递减,求出
上单调递减,求出![]() 的最大值,列出不等数求出解集即为
的最大值,列出不等数求出解集即为![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,函数
时,函数![]() ,
,
则![]() ,
,
![]() 函数
函数![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]()
![]() ,切点为
,切点为![]() ;
;
![]() 函数
函数![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() ;
;
即![]() ;
;
(2)函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
则![]() ;
;
![]() 在
在![]() 上单调递增,
上单调递增,![]() 无极值.
无极值.
(3)由![]() ,得
,得![]() ;
;
又函数![]() 在
在![]() 上单调增函数,
上单调增函数,
则![]() 在
在![]() 上恒成立,
上恒成立,
即不等式![]() 在
在![]() 上恒成立;
上恒成立;
也即![]() 在
在![]() 上恒成立,
上恒成立,
又![]() 在
在![]() 为减函数,
为减函数,
所以![]() (1)
(1)![]() .
.
所以![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】对于以下四个命题:①两条异面直线有无数条公垂线;②直线在平面内的射影是直线;③如果两条直线在同一个平面内的射影平行,那这两条直线平行;④过两条异面直线的一条有且仅有一个平面与已知直线平行;上述命题中为真命题的个数为( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直角,
为直角,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)试用![]() 、
、![]() 表示向量
表示向量![]() ;
;
(2)在线段![]() 上取一点
上取一点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,使得直线
,使得直线![]() 过
过![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,过
,过![]() 作线段
作线段![]() ,使得
,使得![]() 为
为![]() 的中点,且
的中点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
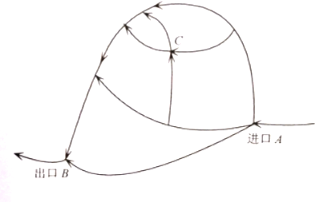
【题目】如图是一旅游景区供游客行走的路线图,假设从进口![]() 开始到出口
开始到出口![]() ,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共
,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共![]() 名游客结伴到旅游景区游玩,他们从进口
名游客结伴到旅游景区游玩,他们从进口![]() 的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口
的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口![]() 集中,设点
集中,设点![]() 是其中的一个交叉路口点.
是其中的一个交叉路口点.
(1)求甲经过点![]() 的概率;
的概率;
(2)设这![]() 名游客中恰有
名游客中恰有![]() 名游客都是经过点
名游客都是经过点![]() ,求随机变量
,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次足球邀请赛共安排了![]() 支球队参加,每支球队预定的比赛场数分别是
支球队参加,每支球队预定的比赛场数分别是![]() ,
,![]() ,…,
,…,![]() .若任两支球队之间至多安排了一场比赛,则称
.若任两支球队之间至多安排了一场比赛,则称![]() 是一个“有效安排”.证明:若
是一个“有效安排”.证明:若![]() 是一个有效安排,且
是一个有效安排,且![]() ,则可去掉一支球队,并重新调整各队之间的对局情况,使
,则可去掉一支球队,并重新调整各队之间的对局情况,使![]() 也是一个有效安排.
也是一个有效安排.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的.在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样.直角坐标系内任意两点![]() ,
,![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:![]() ;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点
;到两点P.Q“距离”相等的点的轨迹称为线段PQ的“垂直平分线”.已知点![]() 、
、![]() 、
、![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]()
![]() 上一点
上一点![]() 到原点
到原点![]() 的“距离”;
的“距离”;
(2)写出线段AB的“垂直平分线”的轨迹方程,并作出大致图像;
(3)定义:若三角形三边的“垂直平分线”交于一点,则该点称为三角形的“外心”.试判断![]() 的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
的“外心”是否存在,如果存在,求出“外心”;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③![]() ;④当
;④当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,正确的个数为( )
,正确的个数为( )
A.1个B.2个C.3个D.以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com