
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)若对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 的两个零点为
的两个零点为![]() ,试判断
,试判断![]() 的正负,并说明理由.
的正负,并说明理由.
【答案】(1)![]() .(2)见解析
.(2)见解析
【解析】试题分析:(1)由![]() 解得
解得![]() .由题可得
.由题可得![]() 在
在![]() 恒成立,分别求得两边函数的值域,运用恒成立思想,即可得到k的范围
恒成立,分别求得两边函数的值域,运用恒成立思想,即可得到k的范围
(2)由题意知,函数![]() ,
, ![]() 是函数
是函数![]() 的两个零点,易得函数
的两个零点,易得函数![]() 在区间在区间
在区间在区间![]() 上单调递减.只需证明
上单调递减.只需证明![]() 即可.
即可.
试题解析: (1)由题得, ![]() ,
,
∵函数在![]() 处的切线方程为
处的切线方程为![]() ,
,
∴![]() ,∴
,∴![]() .
.
依题意, ![]() 对任意的
对任意的![]() 都成立,
都成立,
∴![]() ,即
,即![]() 对任意的
对任意的![]() 都成立,从而
都成立,从而![]() .
.
又不等式整理可得, ![]() .
.
令![]() ,
,
∴![]()
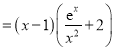 .
.
令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
∴![]() .
.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)结论是![]() .
.
理由如下:由题意知,函数![]() ,
,
∴![]() ,
,
易得函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
∴只需证明![]() 即可.
即可.
∵![]() 是函数
是函数![]() 的两个零点,
的两个零点,
∴![]() 相减,得
相减,得![]() .
.
不妨令![]() ,
,
则![]() ,∴
,∴![]() ,
,
∴![]() ,
, ![]() ,
,
即证![]() ,
,
即证![]() .
.
∵![]()
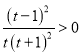 ,
,
∴![]() 在区间
在区间![]() 上单调递增.
上单调递增.
∴![]() .
.
综上所述,函数![]() 总满足
总满足![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M. 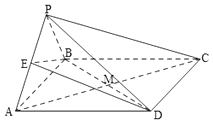
(1)求证:PC∥平面EBD;
(2)求证:BE⊥平面AED.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an+n(n∈N*).
(1)求证数列{an﹣1}是等比数列,并求数列{an}的通项公式;
(2)若bn=log2(﹣an+1),求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x﹣5|.
(1)当a=1时,求f(x)的最小值;
(2)如果对任意的实数x,都有f(x)≥1成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=ax2﹣(2a+1)x+a+1对于a∈[﹣1,1]时恒有f(x)<0,则实数x的取值范围是( )
A.(1,2)
B.(﹣∞,1)∪(2,+∞)
C.(0,1)
D.(﹣∞,0)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力部门需在A、B两地之间架设高压电线,因地理条件限制,不能直接测量A、B两地距离.现测量人员在相距 ![]() km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的
km的C、D两地(假设A、B、C、D在同一平面上)测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度为A、B距离的 ![]() 倍,问施工单位应该准备多长的电线?
倍,问施工单位应该准备多长的电线? 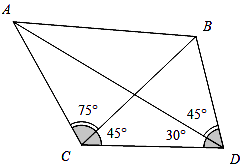
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5.
(1)求数列{an}的通项公式;
(2)设bn=|an|,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3﹣3(a+1)x2+6ax+8,其中a∈R.已知f(x)在x=3处取得极值.
(1)求f(x)的解析式;
(2)求f(x)在点A(1,16)处的切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com