【题目】如图是2017年第一季度中国某五省
情况图，则下列陈述正确的是（ ）
①2017年第一季度 
总量高于4000亿元的省份共有3个；
②与去年同期相比，2017年第一季度五个省的
总量均实现了增长；
③去年同期的
总量前三位依次是
省、
省、
省；
④2016年同期
省的
总量居于第四位．
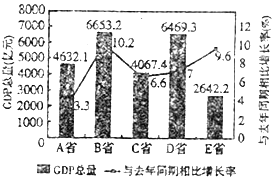
A. ①② B. ②③④ C. ②④ D. ①③④
科目：高中数学 来源： 题型：
【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3，从盒中任取3张卡片．
（Ⅰ）求所取3张卡片上的数字完全相同的概率；
（Ⅱ）
表示所取3张卡片上的数字的中位数，求
的分布列与数学期望．
（注：若三个数
满足
，则称
为这三个数的中位数）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中， 
， 
， 
， 
是
中点（如图1）.将
沿
折起到图2中
的位置，得到四棱锥
.
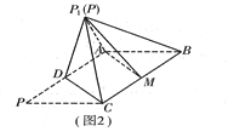
（1）将
沿
折起的过程中， 
平面
是否成立？并证明你的结论；
（2）若
，过
的平面交
于点
，且
为
的中点，求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
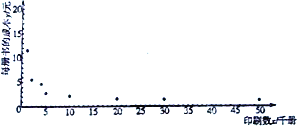
【题目】为研究某种图书每册的成本费
（元）与印刷数
（千册）的关系，收集了一些数据并作了初步处理，得到了下面的散点图及一些统计量的值．
|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中
， 
．
（1）根据散点图判断： 
与
哪一个更适宜作为每册成本费
（元）与印刷数
（千册）的回归方程类型？（只要求给出判断，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立
关于
的回归方程（回归系数的结果精确到0.01）；
（3）若每册书定价为10元，则至少应该印刷多少册才能使销售利润不低于78840元？（假设能够全部售出，结果精确到1）
（附：对于一组数据
， 
，…， 
，其回归直线
的斜率和截距的最小二乘估计分别为
， 
）
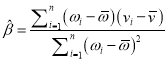查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题共14分）如图，在三棱锥
中， 
底面
，点
， 
分别在棱
上，且
（Ⅰ）求证： 
平面
；（Ⅱ）当
为
的中点时，求
与平面
所成的角的大小；（Ⅲ）是否存在点
使得二面角
为直二面角？并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线l的参数方程为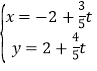
（t为参数），它与曲线
C：（y－2）2－x2＝1交于A、B两点．
（1）求|AB|的长；
（2）在以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为
，求点P到线段AB中点M的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为激发学生学习的兴趣，老师上课时在黑板上写出三个集合：
；然后叫甲、乙、丙三位同学到讲台上，并将“
”中的数告诉了他们，要求他们各用一句话来描述，以便同学们能确定该数，以下是甲、乙、丙三位同学的描述：
甲：此数为小于6的正整数；乙：A是B成立的充分不必要条件；
丙：A是C成立的必要不充分条件
若老师评说这三位同学都说得对，则“”中的数为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
