
【题目】当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 17.3 | 17.9 | 17.3 | 15.8 | 13.7 | 11.6 | 10.06 | 9.5 | 10.06 | 11.6 | 13.7 | 15.8 |
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x-![]() -1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
-1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________(由小到大).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱,现统计了连续![]() 天的售出和收益情况,如下表:
天的售出和收益情况,如下表:
售出水量 |
|
|
|
|
|
收益 |
|
|
|
|
|
(1)若每天售出![]() 箱水,求预计收益是多少元?
箱水,求预计收益是多少元?
(2)期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前![]() 名,获一等奖学金
名,获一等奖学金![]() 元;考入年级前
元;考入年级前![]() 名,获二等奖学金
名,获二等奖学金![]() 元;考入年级
元;考入年级![]() 名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为
名以后的特困生不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
①在学生甲获得奖学金的条件下,求他获得一等奖学金的概率;
②已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额![]() 的分布列及数学期望
的分布列及数学期望
附: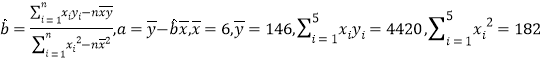
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程](10分)
在极坐标系中,圆C的极坐标方程为![]() ,若以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系.
,若以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系.
(1)求圆C的一个参数方程;
(2)在平面直角坐标系中,![]() 是圆C上的动点,试求
是圆C上的动点,试求![]() 的最大值,并求出此时点P的直角坐标.
的最大值,并求出此时点P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.
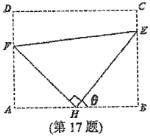
(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车![]() 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度![]() 单位:千米
单位:千米![]() 时
时![]() 是车流密度
是车流密度![]() 单位:辆
单位:辆![]() 千米
千米![]() 的函数
的函数![]() 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆![]() 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆![]() 千米时,车流速度为100千米
千米时,车流速度为100千米![]() 时,研究表明:当
时,研究表明:当![]() 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
![]() Ⅰ
Ⅰ![]() 当
当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
![]() Ⅱ
Ⅱ![]() 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量![]() 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆![]() 时
时![]() 可以达到最大?并求出最大值.
可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查中学生每天玩游戏的时间是否与性别有关,随机抽取了男、女学生各50人进行调查,根据其日均玩游戏的时间绘制了如下的频率分布直方图.
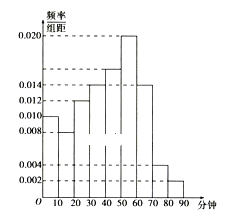
(1)求所调查学生日均玩游戏时间在![]() 分钟的人数;
分钟的人数;
(2)将日均玩游戏时间不低于60分钟的学生称为“游戏迷”,已知“游戏迷”中女生有6人;根据已知条件,完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
非游戏迷 | 游戏迷 | 合计 | |
男 | |||
女 | |||
合计 |
附: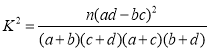 (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (常数
(常数![]() )满足
)满足![]() .
.
(1)求![]() 的值,并对常数
的值,并对常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值.
的最小值.
(3)若方程![]() 在
在![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com