
【题目】设数列{an}的前n项和为Sn , 设an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线y=x+2上.
(Ⅰ)求an , bn;
(Ⅱ)若数列{bn}的前n项和为Bn , 比较 ![]() +
+ ![]() +…+
+…+ ![]() 与1的大小.
与1的大小.
【答案】解:(Ⅰ)∵an是Sn与2的等差中项,∴2an=Sn+2 …①当n=1时,a1=2;
n≥2时,2an﹣1=Sn﹣1+2 …②;
∴由①﹣②得:an=2an﹣1
∴{an}是一个以2为首项,以2为公比的等比数列,
∴an=2n .
又∵点P(bn , bn+1)在直线x﹣y+2=0上,
∴bn﹣bn+1+2=0即:bn+1﹣bn=2,
又b1=1,∴{bn}是一个以1为首项,以2为公差的等差数列,
∴bn=2n﹣1.
(Ⅱ)由(Ⅰ)知:Bn= ![]() .
.
∴ ![]() ,
,
∴ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() =1﹣
=1﹣ ![]() <1
<1
【解析】(I)由于an是Sn与2的等差中项,可得2an=Sn+2,利用当n≥2时,an=Sn﹣Sn﹣1即可得出an与an﹣1的关系,再利用等比数列的通项公式即可得出.由于点P(bn , bn+1)在直线x﹣y+2=0上,可得bn﹣bn+1+2=0即:bn+1﹣bn=2,再利用等差数列的通项公式即可得出.(II)利用等差数列的前n项和公式可得Bn , 再利用“放缩法”和“裂项求和”即可证明
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF= ![]() ,则异面直线AD,BC所成的角的补角为( )
,则异面直线AD,BC所成的角的补角为( ) 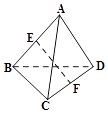
A.120°
B.60°
C.90°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 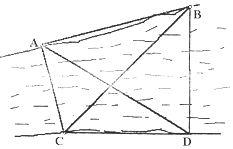
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是各项都为正数的等比数列,{bn}是等差数列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 求数列{Snbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2﹣6x+5与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交于A,B两点,且CA⊥CB求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(Ⅰ)证明:A1C1=AB1;
(Ⅱ)若AC⊥AB1 , ∠BCC1=120°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.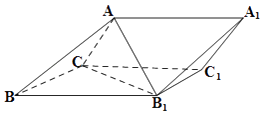
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com