
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
【答案】
(1)解:在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2 ![]() =a﹣2a
=a﹣2a ![]() ,
,
利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),
即 sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,
即sinC=2sinCcosA,∴cosA= ![]() ,∴A=
,∴A= ![]()
(2)解:若a= ![]() ,则由正弦定理可得
,则由正弦定理可得 ![]() =
= ![]() =2,
=2,
∴b+c=2(sinB+sinC)=2[sinB+sin( ![]() ﹣B)]=3sinB+
﹣B)]=3sinB+ ![]() cosB=2
cosB=2 ![]() sin(B+
sin(B+ ![]() ).
).
由于 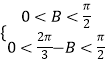 ,求得
,求得 ![]() <B<
<B< ![]() ,∴
,∴ ![]() <B+
<B+ ![]() <
< ![]() .
.
∴sin(B+ ![]() )∈(
)∈( ![]() ,1],∴b+c∈(3,2
,1],∴b+c∈(3,2 ![]() ]
]
【解析】(1)在锐角△ABC中,根据条件利用正弦定理可得 (sinB﹣2sinC)cosA=sinA(﹣cosB),化简可得cosA = ![]() ,由此可得A的值.(2)由正弦定理可得
,由此可得A的值.(2)由正弦定理可得 ![]() =
= ![]() =2,可得 b+c=2(sinB+sinC)=2
=2,可得 b+c=2(sinB+sinC)=2 ![]() sin(B+
sin(B+ ![]() ).
).
再由  ,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.
,求得B的范围,再利用正弦函数的定义域和值域求得b+c的取值范围.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作,政府招聘了200名市民志愿者,按年龄情况进行统计的频率分布表和频率分布直方图如下:
分组(岁) | 频数 | 频率 |
[30,35) | 20 | 0.1 |
[35,40) | 20 | 0.1 |
[40,45) | ① | 0.2 |
[45,50) | ② | ③ |
[50,55] | 40 | 0.2 |
合计 | 200 | 1 |
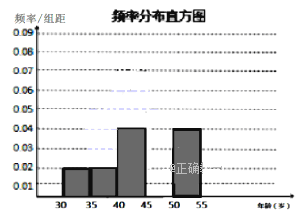
(1)频率分布表中的①②③位置应填什么数?补全频率分布直方图;
(2)根据频率分布直方图估计这200名志愿者的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图表示的算法功能是( )
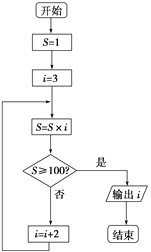
A. 计算小于100的奇数的连乘积
B. 计算从1开始的连续奇数的连乘积
C. 从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数
D. 计算1×3×5×…×n≥100时的最小的n的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 【2016高考新课标Ⅲ文数】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(I)若![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,证明
的中点,证明![]() ;
;
(II)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考山东文数】已知椭圆C:![]() (a>b>0)的长轴长为4,焦距为2
(a>b>0)的长轴长为4,焦距为2![]() .
.
(I)求椭圆C的方程;
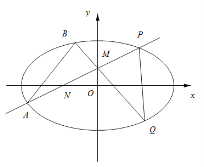
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、k',证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考四川文科】在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为![]() ;当P是原点时,定义P的“伴随点”为它自身,现有下列命题:
;当P是原点时,定义P的“伴随点”为它自身,现有下列命题:
若点A的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点A.
的“伴随点”是点A.
单元圆上的“伴随点”还在单位圆上.
若两点关于x轴对称,则他们的“伴随点”关于y轴对称
④若三点在同一条直线上,则他们的“伴随点”一定共线.
其中的真命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考天津文数】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
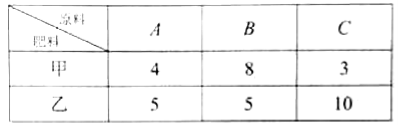
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y计划表示生产甲、乙两种肥料的车皮数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店会员活动日.
(Ⅰ)随机抽取50名会员对商场进行综合评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
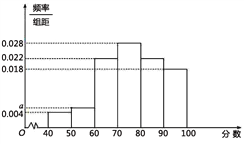
(1)求频率分布直方图中的值;
(2)估计会员对商场的评分不低于80的概率.
(Ⅱ)采取摸球兑奖的方式对会员进行返代金券活动,每位会员从一个装有5个标有面值的球(2个所标的面值为300元,其余3个均为100元)的袋中一次性随机摸出2个球,球上所标的面值之和为该会员所获的代金券金额.求某会员所获得奖励超过400元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人约定在中午12时到下午1时之间到某站乘公共汽车,又知这段时间内有4班公共汽车.设到站时间分别为12:15,12:30,12:45,1:00.如果他们约定:
①见车就乘;
②最多等一辆.
试分别求出在两种情况下两人同乘一辆车的概率.假设甲乙两人到达车站的时间是相互独立的,且每人在中午12点到1点的任意时刻到达车站是等可能的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com