
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
,![]() 为
为![]() 中点.
中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)可证![]() 平面
平面![]() ,从而得到要证的线面垂直;
,从而得到要证的线面垂直;
(2)过点![]() 作
作![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,可证二面角
,可证二面角![]() 的平面角为
的平面角为![]() ,利用余弦定理可求其余弦值后可得其正弦值.我们也可以建立如图所示的空间直角坐标系,求出平面
,利用余弦定理可求其余弦值后可得其正弦值.我们也可以建立如图所示的空间直角坐标系,求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量后可求它们的夹角的余弦值,从而得到二面角的正弦值.
的法向量后可求它们的夹角的余弦值,从而得到二面角的正弦值.
(1)证明:因为![]() ,
,![]() ,
,
所以![]() ,
,
又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,∴ 所以
,∴ 所以![]() ,
,
∵![]() 为
为![]() 中点,且
中点,且![]() 为等边三角形,∴
为等边三角形,∴![]() ,又∵
,又∵![]() ,
,
∴![]() 平面
平面![]() .
.
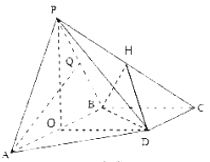
(2)【法一】过点![]() 作
作![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,
,
取![]() 中点为
中点为![]() ,连接
,连接![]() .
.
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
由平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ,由条件知
,由条件知![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,
,
由二面角的定义知,二面角![]() 的平面角为
的平面角为![]() ,
,
在![]() 中,
中,![]() ,
,
由![]() ,所以
,所以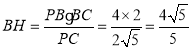 ,
,
同理可得![]() ,
,
又![]() ,在
,在![]() 中,
中,
 ,
,
所以,二面角![]() 的正弦值为
的正弦值为![]() .
.
【法二】
取![]() 中点为
中点为![]() ,连接
,连接![]() ,因为
,因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
由平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,由
,由![]() ,
,![]() ,
,
可知![]() ,所以
,所以![]() ,
,
以![]() 中点
中点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
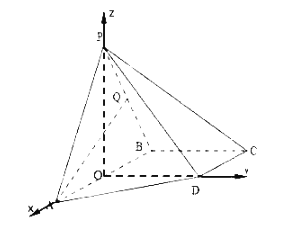
所以![]() ,
,![]() ,
,
所以![]() ,
,
由(1)知,可以![]() 为平面
为平面![]() 的法向量,
的法向量,
因为![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
由(1)知,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由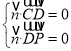 得
得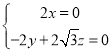 ,
,
取![]() ,则
,则![]() ,
,
所以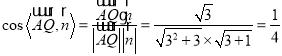 ,
,
所以二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 | [85,90) | [90,95) | [95,100) | [100,105) | [105,110) |
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在[90,95)内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂一种溶液的成品,生产过程的最后工序是过滤溶液中的杂质,过滤初期溶液含杂质为2%,每经过一次过滤均可使溶液杂质含量减少![]() ,记过滤次数为x(
,记过滤次数为x(![]() )时溶液杂质含量为y.
)时溶液杂质含量为y.
(1)写出y与x的函数关系式;
(2)按市场要求,出厂成品杂质含量不能超过0.1%,问至少经过几次过滤才能使产品达到市场要求?(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知![]() ,
, ![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
, ![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当直线
,当直线![]() 绕点
绕点![]() 转动时,试判断以
转动时,试判断以![]()
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数.
的积函数.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰好为
的值域恰好为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为![]() .
.

(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com