
现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为 ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.
(1)求该射手恰好命中一次的概率.
(2)求该射手的总得分X的分布列.
科目:高中数学 来源: 题型:解答题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,问从2号箱取出红球的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
| 参考数据 | 当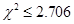 时,无充分证据判定变量 时,无充分证据判定变量 有关联,可以认为两变量无关联; 有关联,可以认为两变量无关联; |
当 时,有 时,有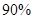 把握判定变量 把握判定变量 有关联; 有关联; | |
当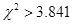 时,有 时,有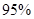 把握判定变量 把握判定变量 有关联; 有关联; | |
当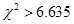 时,有 时,有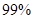 把握判定变量 把握判定变量 有关联. 有关联. |
 ,其中
,其中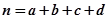 .)
.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了提高食品的安全度,某食品安检部门调查了一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长速度(1.0~1.2 kg/年)的比例超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题.
| 鱼的 质量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 鱼的 条数 | 3 | 20 | 35 | 31 | 9 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有7道题,其中5道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的两道题都是甲类题的概率;
(2)所取的两道题不是同一类题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校为组建校篮球队,对报名同学进行定点投篮测试,规定每位同学最多投3次,每次在A或B处投篮,在A处投进一球得3分,在B处投进一球得2分,否则得0分,每次投篮结果相互独立,将得分逐次累加并用X表示,如果X的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮方案有以下两种:
方案1:先在A处投一球,以后都在B处投;
方案2:都在B处投篮.
已知甲同学在A处投篮的命中率为0.4,在B处投篮的命中率为0.6.
(1)甲同学若选择方案1,求X=2时的概率;
(2)甲同学若选择方案2,求X的分布列和数学期望;
(3)甲同学选择哪种方案通过测试的可能性更大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为 ,乙投进的概率为
,乙投进的概率为 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=x2+bx+c,其中b,c是某范围内的随机数,分别在下列条件下,求事件A“f(1)≤5且f(0)≤3”发生的概率.
(1)若随机数b,c∈{1,2,3,4}.
(2)已知随机函数Rand( )产生的随机数的范围为{x|0≤x≤1},b,c是算法语句b="4*Rand(" )和c="4*Rand(" )的执行结果.(注:符号“*”表示“乘号”)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com