
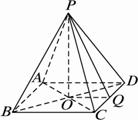
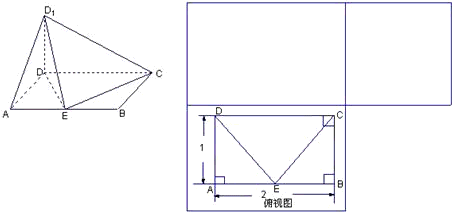
(1)求PC与平面PBD所成角的大小;
(2)求![]() 的值;
的值;
(3)求四棱锥P—ABCD夹在平面ADE与底面ABCD之间部分的体积.

解:(1)在平面ABCD内作CG⊥BD于G,连结PG,
∵PD⊥平面ABCD,CG![]() 平面ABCD,
平面ABCD,
∴PD⊥CG.
∴CG⊥平面PBD.
∴∠CPG就是PC与面PBD所成的角.
在Rt△BCD中,CG=![]() ,
,
又PC=![]() ,
,
故在Rt△PGC中,sinCPG=![]() .
.
又∵∠CPG为锐角,
∴∠CPG=arcsin![]() .
.
∴PC与平面PBD所成的角为arcsin![]() .
.
(2)设平面ADE与PC交于F,连DF、EF,
∵PC⊥平面ADE,DF![]() 平面ADE,∴PC⊥DF.
平面ADE,∴PC⊥DF.
又∴PD=DC,∴F为PC中点.
∵BC∥AD,BC![]() 平面ADE.
平面ADE.
∴BC∥平面ADE,
又平面ADE∩平面PBC=EF.
∴BC∥EF.
∴E为PB中点,故![]() =1.
=1.
(3)∵PD⊥平面ABCD,∴PD⊥AD.
又AD⊥DC,∴AD⊥平面PDC.
又DF![]() 平面PDC,∴AD⊥DF,
平面PDC,∴AD⊥DF,
∵EF∥BC,BC∥AD,∴EF∥AD.
又PF⊥平面ADEF,EF=![]() BC=1,DF=
BC=1,DF=![]() DC=
DC=![]() ,
,
∴VP—DAEF=![]()
又VP—ABCD=![]() ×(2×
×(2×![]() )×
)×![]() =8,
=8,
∴V=VP—ABCD-VP—DAEF=5,
即四棱锥P—ABCD夹在平面ADE与底面ABCD之间部分的体积为5.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)![]() =
= ![]() +x
+x![]() +y
+y![]() ;??
;??
(2) ![]() =x
=x![]() +y
+y![]() +
+![]() .?
.?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com