
分析 (Ⅰ)作出函数的图象,即可求f(x)的值域;
(Ⅱ)利用柯西不等式,即可证明结论.
解答 (Ⅰ)解:函数f(x)=|x-$\frac{1}{2}$|-|2x+1|=$\left\{\begin{array}{l}{x+\frac{3}{2},x<-\frac{1}{2}}\\{-3x-\frac{1}{2},-\frac{1}{2}≤x≤\frac{1}{2}}\\{-x-\frac{3}{2},x>\frac{1}{2}}\end{array}\right.$,
函数的图象如图所示,则函数的值域为(-∞,1];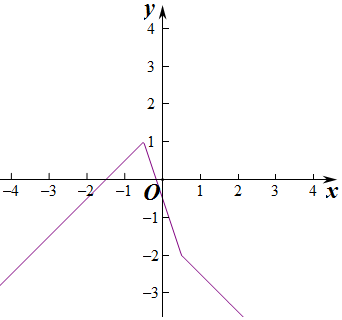
(Ⅱ)证明:由题意x,y,z均为正实数,x+y+z=1,
由柯西不等式可得(x+y+z)($\frac{{y}^{2}}{x}$+$\frac{{z}^{2}}{y}$+$\frac{{x}^{2}}{z}$)≥(y+z+z)2=1,
∴$\frac{{y}^{2}}{x}$+$\frac{{z}^{2}}{y}$+$\frac{{x}^{2}}{z}$≥1.
点评 本题考查绝对值函数的值域,考查不等式的证明,考查柯西不等式,属于中档题.


科目:高中数学 来源: 题型:选择题
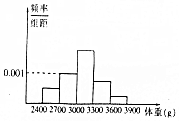
| A. | 0.001 | B. | 0.1 | C. | 0.2 | D. | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 价格 | 5000元及以上 | 3000元-4999元 | 1000元-2999元 | 1000元以下 |
| 45岁及以下 | 12 | 28 | 66 | 4 |
| 45岁以上 | 3 | 17 | 46 | 24 |
| P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
| k | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校300名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩的众数、平均分分别为( )
某校300名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩的众数、平均分分别为( )| A. | 60、69 | B. | 65、71 | C. | 65、73 | D. | 60、75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中正确是①④.(填序号即可)
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中正确是①④.(填序号即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com