
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
(1) a=2 (2) (-∞,5]
【解析】(1)由f(x)≤3,得|x-a|≤3,解得a-3≤x≤a+3.
又已知不等式f(x)≤3的解集为{x|-1≤x≤5},
所以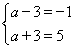 解得a=2.
解得a=2.
(2)方法一:当a=2时,f(x)=|x-2|,
设g(x)=f(x)+f(x+5)=|x-2|+|x+3|.
由|x-2|+|x+3|≥|(x-2)-(x+3)|=5,
当且仅当-3≤x≤2时等号成立,得g(x)的最小值为5.
从而,若f(x)+f(x+5)≥m对一切实数x恒成立,实数m的取值范围为(-∞,5].
方法二:当a=2时,f(x)=|x-2|,设g(x)=f(x)+f(x+5)=|x-2|+|x+3|.
于是g(x)=|x-2|+|x+3|=
所以当x<-3时,g(x)>5;
当-3≤x≤2时,g(x)=5;
当x>2时,g(x)>5.
综上可得,g(x)的最小值为5.
从而,若f(x)+f(x+5)≥m对一切实数x恒成立,实数m的取值范围为(-∞,5].


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(解析版) 题型:填空题
已知命题:若数列{an}为等差数列,且am=a,an=b(m≠n,m、n∈N*),则am+n=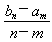 ;现已知等比数列{bn}(bn>0,n∈N*), bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.
;现已知等比数列{bn}(bn>0,n∈N*), bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:解答题
已知函数f(x)=ln x+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
A.?x∈R,f(x)≤f(x0)
B.-x0是f(-x)的极小值点
C.-x0是-f(x)的极小值点
D.-x0是-f(-x)的极小值点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:解答题
设f(x)=|lg x|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b)=2f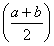 ,
,
求证:a·b=1,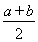 >1.
>1.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:选择题
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16 B.-16
C.a2-2a-16 D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:解答题
(13分)已知圆O:x2+y2=3的半径等于椭圆E: =1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-
=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).

(1)求椭圆E的方程;
(2)求证:|AF|-|BF|=|BM|-|AM|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com