
 ,y1+y2=2,因此p=1.
,y1+y2=2,因此p=1. ,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.
,y1+y2=2m所以p=m,将直线方程与抛物线的方程联立,判别式大于0求出m的范围.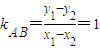 ,y1+y2=2m
,y1+y2=2m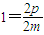
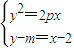 消去x得
消去x得

科目:高中数学 来源: 题型:阅读理解
| y1-y2 | x1-x2 |
查看答案和解析>>
科目:高中数学 来源:陕西省师大附中2012届高三第四次模拟考试数学理科试题 题型:044
已知抛物线y2=4x,点M(1,0)关于y轴的对称点为N,直线l过点M交抛物线于A,B两点.
(1)证明:直线NA,NB的斜率互为相反数;
(2)求△ANB面积的最小值;
(3)当点M的坐标为(m,0),(m>0)且m≠1.根据(1)(2)推测并回答下列问题(不必说明理由):
①直线NA,NB的斜率是否互为相反数?
②△ANB面积的最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
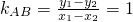 ,y1+y2=2,因此p=1.
,y1+y2=2,因此p=1.查看答案和解析>>
科目:高中数学 来源:浦东新区二模 题型:填空题
| y1-y2 |
| x1-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com