
【题目】设![]() 为整数,若对任意的
为整数,若对任意的![]() ,不等式
,不等式![]() 恒成立,则
恒成立,则![]() 的最大值是__________.
的最大值是__________.
【答案】1
【解析】
由题意先代入x=1求得a的范围,要满足题意,则a![]() 是必要条件,又
是必要条件,又![]() 为整数,只需再验证a=1时,不等式恒成立即可,构造函数g(x)
为整数,只需再验证a=1时,不等式恒成立即可,构造函数g(x)![]() ,x∈
,x∈![]() ,通过求导求得最小值,证明结论成立.
,通过求导求得最小值,证明结论成立.
由题意对任意的![]() ,不等式
,不等式![]() 恒成立,则x=1时,不等式
恒成立,则x=1时,不等式![]() 也成立,
也成立,
代入x=1得e+3![]() ,又
,又![]() 为整数,则a
为整数,则a![]() ,这是满足题意的一个必要条件,又
,这是满足题意的一个必要条件,又![]() 为整数,
为整数,
只需验证a=1时,对任意的![]() ,不等式
,不等式![]() 恒成立,
恒成立,
即证![]() ,变形为
,变形为![]() 对任意的
对任意的![]() 恒成立,
恒成立,
令g(x)![]() ,x∈
,x∈![]() ,
,
则g′(x)![]() ,在(0,1)上小于0,在(1,
,在(0,1)上小于0,在(1,![]() )上大于0,
)上大于0,
故g(x)在(0,1)递减,在(1,![]() )递增,∴g(x)
)递增,∴g(x)![]() g(1)=3>0,
g(1)=3>0,
∴![]() 对任意的
对任意的![]() 恒成立,
恒成立,
故a=1满足题意.
故答案为1.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.
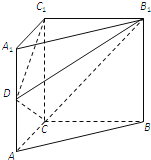
(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在湖南师大附中的校园歌手大赛决赛中,有6位参赛选手(1号至6号)登台演出,由现场的100位同学投票选出最受欢迎的歌手,各位同学须彼此独立地在投票器上选出3位侯选人,其中甲同学是1号选手的同班同学,必选1号,另在2号至6号选手中随机选2名;乙同学不欣赏2号选手,必不选2号,在其他5位选手中随机选出3名;丙同学对6位选手的演唱没有偏爱,因此在1号至6号选手中随机选出3名.
(1)求同学甲选中3号且同学乙未选中3号选手的概率;
(2)设3号选手得到甲、乙、丙三位同学的票数之和为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线
的直线与抛物线![]() 相切,设第一象限的切点为
相切,设第一象限的切点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于两点
相交于两点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆过点
为直径的圆过点![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,四边形ADEF为正方形,AD∥BC,AD⊥AB,AD=2BC=2.
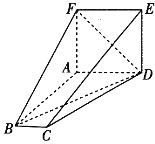
(1)证明:平面ADEF⊥平面ABF.
(2)若平面ADEF⊥平面ABCD,二面角A-BC-E为30°,三棱锥A-BDF的外接球的球心为O,求异面直线OC与DF所成角的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com