分析:(1)由题意判断点M的轨迹是以F
1,F
2为焦点的椭圆,进而可求点M的轨迹C的方程;
(2)设直线l的方程为y=x+n,代入椭圆方程,利用△>0及韦达定理,结合
•=0,即可求得直线l的方程.
解答:解:(1)由题意得,F
1(-1,0),F
2(1,0),圆F
1的半径为
2,且|MF
2|=|MP|…(1分)
从而
|MF1|+|MF2|=|MF1|+|MP|=|PF1|=2>|F1F2|…(3分)
∴点M的轨迹是以F
1,F
2为焦点的椭圆,…(5分)
其中长轴
2a=2,得到
a=,焦距2c=2,则短半轴b=1
椭圆方程为:
+y2=1…(6分)
(2)设直线l的方程为y=x+n,由
可得3x
2+4nx+2n
2-2=0…(8分)
则△=16n
2-24(n
2-1)>0,即n
2<3①…(9分)
设A(x
1,y
1),B(x
2,y
2),则
x1+x2=,x1x2=由
•=0可得x
1x
2+y
1y
2=0,即x
1x
2+(x
1+n)(x
2+n)=0…(10分)
整理可得
2x1x2+n(x1+x2)+n2=0化简可得3n
2=4,满足①式,故直线]l的方程为:
y=x±…(12分)
点评:本题考查椭圆的定义,考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是利用椭圆的定义,联立直线与椭圆方程,属于中档题.

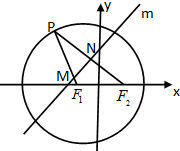 已知点P是圆F1:(x+1)2+y2=8上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线m分别与PF1、PF2交于M、N两点.
已知点P是圆F1:(x+1)2+y2=8上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线m分别与PF1、PF2交于M、N两点.

 上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点.
上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点. 上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点.
上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点.