
【题目】已知集合A={1,2},B={x|(x2+ax)(x2+ax+2)=0},记集合A中元素的个数为n(A),定义m(A,B)= ![]() ,若m(A,B)=1,则正实数a的值是 .
,若m(A,B)=1,则正实数a的值是 .
【答案】![]()
【解析】解:由于(x2+ax)(x2+ax+2)=0等价于
x2+ax=0 ①或x2+ax+2=0 ②,
又由A={1,2},且m(A,B)=1,
∴集合B要么是单元素集合,要么是三元素集合,
1°集合B是单元素集合,则方程①有两相等实根,②无实数根,
∴a=0;
2°集合B是三元素集合,则方程①有两不相等实根,②有两个相等且异于①的实数根,
即 ![]() ,
,
解得a=±2 ![]() ,
,
综上所述a=0或a=±2 ![]() ,
,
∵a>0,∴a= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】认真审题,首先需要了解集合的表示方法-特定字母法(①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)为R上的偶函数,g(x)为R上的奇函数,且f(x)+g(x)=log4(4x+1).
(1)求f(x),g(x)的解析式;
(2)若函数h(x)=f(x)﹣ ![]() 在R上只有一个零点,求实数a的取值范围.
在R上只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° 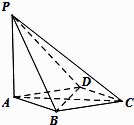
(1)若PA=AB,求PB与平面PDC所成角的正弦值;
(2)当平面PBC与平面PDC垂直时,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣2x+3 (Ⅰ)若函数 ![]() 的最小值为3,求实数m的值;
的最小值为3,求实数m的值;
(Ⅱ)若对任意互不相同的x1 , x2∈(2,4),都有|f(x1)﹣f(x2)|<k|x1﹣x2|成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,若其图象向左平移
)的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于点(﹣ ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2, ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com