
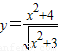 的最小值为2
的最小值为2
 =
= +
+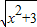 ,
, +
+ ≥2
≥2 =2,
=2,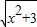
 ,所以不等号的等号不能取到,故最小值不是2,故④不正确
,所以不等号的等号不能取到,故最小值不是2,故④不正确

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:设计必修二数学人教A版 人教A版 题型:013
平面α与β平行,且a![]() α,下列四个命题中
α,下列四个命题中
①a与β内的所有直线平行;
②a与β内的无数条直线平行;
③α与β内的任何一条直线都不垂直;
④α与β无公共点.
其中真命题的个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
①a与β内的所有直线平行;②a与β内的无数条直线平行;③α与β内的任何一条直线都不垂直;④α与β无公共点.其中真命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题中:①a+b≥2![]() ②sin2x+
②sin2x+![]() ≥4 ③设x,y都是正数,若
≥4 ③设x,y都是正数,若![]() =1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
=1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com