已知四面体A-BCD,AB=4,CD=2,AB与CD之间的距离为3,则四面体ABCD体积的最大值为 .
【答案】
分析:作BE平行CD,且BE=CD,连接CE,AE,四面体ABCD的体积=四面体ADBE的体积,由AB与CD之间的距离为3,知四面体ADBE以△ABE为底时的高h=3,要使四面体ADBE体积最大,则△ABE面积要最大,当∠ABE=90°时,△ABE的面积取最大值S=4.由此能求出四面体ABCD体积的最大值.
解答:解:如图,作BE平行CD,且BE=CD,连接CE,AE,

∵BE∥CD,且BE=CD,
∴BECD是平行四边形,
∴A-BDE与A-BCD等底同高,
∴四面体ABCD的体积=四面体ADBE的体积,
∵BE∥CD,
∴AB与CD的公垂线一定垂直面ABE,
∵AB与CD之间的距离为3,
∴四面体ADBE以△ABE为底时的高h=3,
要使四面体ADBE体积最大,则△ABE面积要最大,
∵

=

=4sin∠ABE.
∴当∠ABE=90°时,△ABE的面积取最大值S=4.
∴四面体ABCD体积的最大值=四面体ADBE体积最大值=

=

.
故答案为:4.
点评:本题考查三棱锥的体积的最大值的求法,是基础题.解题时要认真审题,仔细解答,注意合理地通知等价转化.




 =
= .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案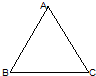 已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )
已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )